펜윅트리 (Fenwick Tree, Binary Indexed Tree, BIT)
펜윅트리는 트리 구조를 1차원 배열로 구현한 자료구조로, 각 위치에서 특정 구간을 대표하는 값을 저장하여 빠르게 구간 합 등을 계산할 수 있다. 업데이트와 쿼리 연산의 시간 복잡도는 O(logN)이다. 1기반 인덱싱을 사용하기 때문에 배열의 크기를 N + 1 (N은 데이터의 크기)로 설정하는 경우가 많다. 세그먼트 트리보다 상대적으로 구현이 간단하고 메모리 사용량이 적다.
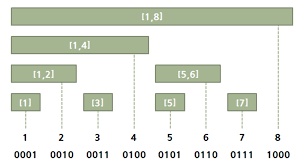
주요 연산 비교
| 연산 | 펜윅 트리 | 세그먼트 트리 |
| 구간 쿼리 | O(logN) | O(logN) |
| 단일 업데이트 | O(logN) | O(logN) |
| 구간 업데이트 | O(NlogN) | O(logN) (Lazy Propagation 사용 시) |
| 메모리 사용량 | O(N) | O(4 * N) |
펜윅 트리 코드
#include <iostream>
#include <vector>
using namespace std;
class FenwickTree {
vector<int> tree;
public:
FenwickTree(int n) : tree(n + 1, 0) {}
void update(int idx, int val) {
while(idx < tree.size()) {
tree[idx] += val;
idx += (idx & -idx); // 상위 인덱스로
}
}
int query(int idx) {
int sum = 0;
while(idx > 0) {
sum += tree[idx];
idx -= (idx & -idx); // 하위 인덱스로
}
return sum;
}
int rangeQuery(int left, int right) {
return query(right) - query(left - 1);
}
};
int main() {
FenwickTree fenwick(10);
fenwick.update(3, 5);
fenwick.update(5, 2);
cout << "Sum from index 1 to 5: " << fenwick.rangeQuery(1, 5) << endl;
return 0;
}(idx & -idx)란?
idx += (idx & -idx), idx -= (idx & -idx)는 펜윅 트리에서 사용하는 연산으로, 현재 인덱스를 기준으로 다음 업데이트할 인덱스를 찾는 방식이다. 이 연산은 펜윅 트리의 구조적인 특징을 이용해 효율적으로 특정 인덱스를 이동하게 한다.
1. 비트 연산의 의미
idx & -idx는 idx의 가장 낮은 비트를 추출하는 연산이다.
- 2의 보수: -idx는 idx의 2의 보수이다. 2의 보수는 모든 비트를 뒤집고 1을 더한 값이므로 idx와 -idx는 공통으로 가장 낮은 비트 하나만 켜진 상태가 된다.
- 비트 AND 연산: idx & -idx는 idx에서 가장 낮은 비트를 남겨두고 나머지는 모두 0으로 만드는 연산이다.
2. 해당 연산이 펜윅 트리에서 사용되는 이유
펜윅 트리는 누적합을 저장하여 특정 인덱스까지의 합을 빠르게 계산할 수 있는 자료구조이다. 각 노드는 특정 구간의 합을 저장하며, 인덱스를 이동하면서 필요한 값만 업데이트하거나 조회할 수 있다. tree[i]의 의미는 인덱스 (i - (i & -i) + 1)부터 i까지의 합을 의미한다는 걸 알면 이해하기 더 쉬울 수도 있다.
업데이트 시 (idx += idx & -idx)
- 업데이트 할 때 idx += idx & -idx를 사용하여 현재 인덱스에서 다음 인덱스로 이동한다.
- 이 연산은 idx에 가장 낮은 비트를 더해주므로, 상위 구간으로 이동하게 된다. 이는 구간을 구성하는 범위를 확장해나가는 과정이라고 볼 수 있다.
쿼리 시 ( idx -= idx & -idx)
- 특정 구간 합을 구할 때는 idx -= idx & -idx을 사용하여 하위 구간으로 이동하면서 필요한 값을 누적한다.
선택 기준
| 상황 | 권장 자료구조 | 설명 |
| 단일 요소 업데이트와 구간 합 | 펜윅트리 | 간단한 구간 합 문제에서는 펜윅트리가 적합 |
| 구간 업데이트와 구간 쿼리 | 세그먼트 트리 | Lazy Propagation으로 효율적인 구간 업데이트 가능 |
| 복잡한 구간 연산 (최대, 최소 등) | 세그먼트 트리 | 다양한 연산 지원 |
| 메모리 사용이 제한적인 경우 | 펜윅 트리 | 메모리 사용량이 적음 |
구간 합 구하기 문제에서의 성능 비교
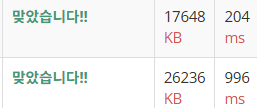
위가 펜윅 트리, 아래가 세그먼트 트리를 이용하여 푼 결과이다. 단순 구간합을 이용할 때는 펜윅트리가 더 성능이 좋다는 것을 확인할 수 있었다.
https://www.acmicpc.net/problem/2042
'자료구조 및 알고리즘' 카테고리의 다른 글
| [자료구조 및 알고리즘] 오일러 경로 테크닉 (1) | 2024.11.27 |
|---|---|
| [자료구조 및 알고리즘] 강한 연결 요소 (Strongly Connected Component, SCC) (0) | 2024.11.15 |
| [자료구조 및 알고리즘] 그래프에서 음의 사이클 구하기 (벨만 포드 알고리즘, 플로이드 워셜 알고리즘) (0) | 2024.11.02 |
| [자료구조 및 알고리즘] 느리게 갱신되는 세그먼트 트리 (Lazy Propagation) (2) | 2024.10.18 |
| [자료구조 및 알고리즘] 세그먼트 트리 (4) | 2024.10.18 |
펜윅트리 (Fenwick Tree, Binary Indexed Tree, BIT)
펜윅트리는 트리 구조를 1차원 배열로 구현한 자료구조로, 각 위치에서 특정 구간을 대표하는 값을 저장하여 빠르게 구간 합 등을 계산할 수 있다. 업데이트와 쿼리 연산의 시간 복잡도는 O(logN)이다. 1기반 인덱싱을 사용하기 때문에 배열의 크기를 N + 1 (N은 데이터의 크기)로 설정하는 경우가 많다. 세그먼트 트리보다 상대적으로 구현이 간단하고 메모리 사용량이 적다.

주요 연산 비교
| 연산 | 펜윅 트리 | 세그먼트 트리 |
| 구간 쿼리 | O(logN) | O(logN) |
| 단일 업데이트 | O(logN) | O(logN) |
| 구간 업데이트 | O(NlogN) | O(logN) (Lazy Propagation 사용 시) |
| 메모리 사용량 | O(N) | O(4 * N) |
펜윅 트리 코드
#include <iostream>
#include <vector>
using namespace std;
class FenwickTree {
vector<int> tree;
public:
FenwickTree(int n) : tree(n + 1, 0) {}
void update(int idx, int val) {
while(idx < tree.size()) {
tree[idx] += val;
idx += (idx & -idx); // 상위 인덱스로
}
}
int query(int idx) {
int sum = 0;
while(idx > 0) {
sum += tree[idx];
idx -= (idx & -idx); // 하위 인덱스로
}
return sum;
}
int rangeQuery(int left, int right) {
return query(right) - query(left - 1);
}
};
int main() {
FenwickTree fenwick(10);
fenwick.update(3, 5);
fenwick.update(5, 2);
cout << "Sum from index 1 to 5: " << fenwick.rangeQuery(1, 5) << endl;
return 0;
}(idx & -idx)란?
idx += (idx & -idx), idx -= (idx & -idx)는 펜윅 트리에서 사용하는 연산으로, 현재 인덱스를 기준으로 다음 업데이트할 인덱스를 찾는 방식이다. 이 연산은 펜윅 트리의 구조적인 특징을 이용해 효율적으로 특정 인덱스를 이동하게 한다.
1. 비트 연산의 의미
idx & -idx는 idx의 가장 낮은 비트를 추출하는 연산이다.
- 2의 보수: -idx는 idx의 2의 보수이다. 2의 보수는 모든 비트를 뒤집고 1을 더한 값이므로 idx와 -idx는 공통으로 가장 낮은 비트 하나만 켜진 상태가 된다.
- 비트 AND 연산: idx & -idx는 idx에서 가장 낮은 비트를 남겨두고 나머지는 모두 0으로 만드는 연산이다.
2. 해당 연산이 펜윅 트리에서 사용되는 이유
펜윅 트리는 누적합을 저장하여 특정 인덱스까지의 합을 빠르게 계산할 수 있는 자료구조이다. 각 노드는 특정 구간의 합을 저장하며, 인덱스를 이동하면서 필요한 값만 업데이트하거나 조회할 수 있다. tree[i]의 의미는 인덱스 (i - (i & -i) + 1)부터 i까지의 합을 의미한다는 걸 알면 이해하기 더 쉬울 수도 있다.
업데이트 시 (idx += idx & -idx)
- 업데이트 할 때 idx += idx & -idx를 사용하여 현재 인덱스에서 다음 인덱스로 이동한다.
- 이 연산은 idx에 가장 낮은 비트를 더해주므로, 상위 구간으로 이동하게 된다. 이는 구간을 구성하는 범위를 확장해나가는 과정이라고 볼 수 있다.
쿼리 시 ( idx -= idx & -idx)
- 특정 구간 합을 구할 때는 idx -= idx & -idx을 사용하여 하위 구간으로 이동하면서 필요한 값을 누적한다.
선택 기준
| 상황 | 권장 자료구조 | 설명 |
| 단일 요소 업데이트와 구간 합 | 펜윅트리 | 간단한 구간 합 문제에서는 펜윅트리가 적합 |
| 구간 업데이트와 구간 쿼리 | 세그먼트 트리 | Lazy Propagation으로 효율적인 구간 업데이트 가능 |
| 복잡한 구간 연산 (최대, 최소 등) | 세그먼트 트리 | 다양한 연산 지원 |
| 메모리 사용이 제한적인 경우 | 펜윅 트리 | 메모리 사용량이 적음 |
구간 합 구하기 문제에서의 성능 비교

위가 펜윅 트리, 아래가 세그먼트 트리를 이용하여 푼 결과이다. 단순 구간합을 이용할 때는 펜윅트리가 더 성능이 좋다는 것을 확인할 수 있었다.
https://www.acmicpc.net/problem/2042
'자료구조 및 알고리즘' 카테고리의 다른 글
| [자료구조 및 알고리즘] 오일러 경로 테크닉 (1) | 2024.11.27 |
|---|---|
| [자료구조 및 알고리즘] 강한 연결 요소 (Strongly Connected Component, SCC) (0) | 2024.11.15 |
| [자료구조 및 알고리즘] 그래프에서 음의 사이클 구하기 (벨만 포드 알고리즘, 플로이드 워셜 알고리즘) (0) | 2024.11.02 |
| [자료구조 및 알고리즘] 느리게 갱신되는 세그먼트 트리 (Lazy Propagation) (2) | 2024.10.18 |
| [자료구조 및 알고리즘] 세그먼트 트리 (4) | 2024.10.18 |
