느리게 갱신되는 세그먼트 트리 (Lazy Propagation)
느리게 갱신되는 세그먼트 트리(Lazy Propagation)는 세그먼트 트리에서 구간 업데이트를 더 효율적으로 처리하기 위해 사용하는 기법이다. 구간의 여러 값을 한 번에 갱신하고, 그 후에 구간에 대한 정보를 빠르게 얻어야 할 때 사용된다.
1. 느리게 갱신되는 세그먼트 트리란?
기본 세그먼트 트리는 특정 구간의 값(합, 최대값 등)을 빠르게 쿼리할 수 있게 해준다. 그런데 만약 구간 내 모든 값에 동일한 연산(ex. 더하기)을 여러 번 적용해야 하는 경우, 기본 세그먼트 트리로는 비효율적일 수 있다. 최악의 경우 nlogn의 시간이 걸릴 수 있기 때문이다. 이때 느리게 갱신되는 세그먼트 트리를 사용하면 구간 전체에 대한 업데이트를 지연시키고 나중에 한꺼번에 처리할 수 있다.
이를테면, 배열 [1, 2, 3, 4, 5] 가 있다. 그리고 3번째에서 5번째까지 모든 값에 2를 더하는 작업을 한다면, 기본 세그먼트 트리에서는 매번 그 범위의 값을 전부 순회하면서 하나씩 더해줘야 한다. 이런 작업이 반복되면 비효율적일 것이다.
느리게 갱신되는 세그먼트 트리는 이런 작업을 즉시 처리하지 않고 지연시켜 두었다가 필요할 때 한꺼번에 처리한다. 이렇게 하면 불필요한 계산을 줄요 효율적으로 구간 업데이트를 처리할 수 있다.
2. 어떤 경우에 사용하는지
느리게 갱신되는 세그먼트 트리는 구간 전체에 대해 일괄적인 업데이트가 자주 발생하는 경우에 사용해야 한다.
- 구간 내 모든 값에 더하기/빼기와 같은 연산을 적용하는 경우
- 대규모 배열에서 구간 내 값들을 일일이 업데이트하는 대신 한꺼번에 처리하고자 할 때
이처럼 여러 값에 대해 동일한 작업을 반복해야 할 때, 느리게 갱신되는 세그먼트 트리는 업데이트와 쿼리를 모두 효율적으로 처리할 수 있다.
3. 느리게 갱신되는 세그먼트 트리의 작동 원리
기본 세그먼트 트리에서는 값이 변경될 때 바로 트리의 모든 관련 노드에 반영한다. 하지만 느리게 갱신되는 세그먼트 트리에서는 lazy 배열을 사용해 변경 사항을 나중에 한꺼번에 반영한다. 이 방법으로 필요할 때만 값을 갱신해 시간을 절약한다.
작동순서
- 구간 업데이트 요청이 들어오면, 해당 구간에 대한 업데이트를 즉시 처리하지 않고 lazy 배열에 변경 사항을 저장해 둔다.
- 그 후 해당 구간에 쿼리 요청이 들어오면, 그때 lazy 배열에 저장된 값을 트리에 반영하여 한꺼번에 처리한다.
- 이 과정을 통해 구간 업데이트를 지연시키고 나중에 필요할 때만 한 번에 갱신하므로, 시간 복잡도를 줄일 수 있다.
예시 상황
- 배열: [1, 2, 3, 4, 5]
- 트리를 초기화하고 나면 이 배열을 세그먼트 트리로 변환해서 관리한다.
- 2번째부터 4번째 값에 3을 더하는 작업을 한다고 가정
- 그 후 1번째부터 5번째 값의 합을 구하는 쿼리를 처리
1. 초기 상태
초기 배열은 [1, 2, 3, 4, 5]이다. 세그먼트 트리는 다음과 같이 초기화된다. 트리 구조에서는 부모 노드가 자식 노드들의 합을 가지고 있다.
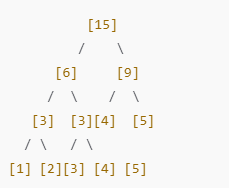
- 루트 노드 15는 전체 배열의 합인 1 + 2 + 3 + 4 + 5 = 15이다.
- 각 리프 노드는 배열의 개별 값을 나타낸다.
2. 구간 업데이트 요청 (2번째부터 4번째까지의 값에 3을 더하기)
이제 2번째부터 4번째 값에 3을 더하는 작업이 들어온다. 이때 트리 전체를 바로 갱신하지 않고 lazy propagation을 이용해 lazy 배열에 값을 저장해서 나중에 처리한다.
- 2번째부터 4번째 구간을 포함하는 노드들의 lazy 값을 업데이트한다.
- 즉, 구간을 나누어 담당하는 노드들에 대해 "나중에 이 값에 3을 더하겠다"는 정보를 lazy 배열에 저장한다.

3. 구간 합 쿼리 요청 (1번째부터 5번째까지의 합 구하기)
이제 1번째부터 5번째 구간 합을 구하는 쿼리가 들어온다. 이때 쿼리 전에, lazy 배열에 저장된 값을 트리에 반영한다.
- 루트 노드로부터 시작해 트리를 내려가면서 lazy 값을 적용한다.
- [2, 4] 구간에 3을 더하라는 지연된 작업이 있으므로 이를 적용한 후 쿼리를 처리한다.
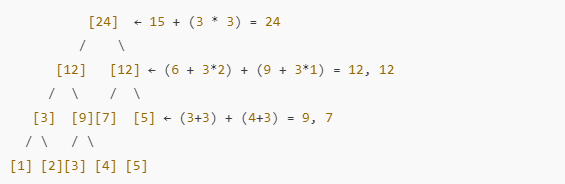
- lazy 값을 반영: 2번째부터 4번째 구간에 각각 3을 더해야 하므로, [2,4] 구간에 해당하는 노드들에 대해 3을 더한 후 트리 값을 업데이트한다.
- 쿼리 처리: lazy 값이 반영된 후, 최종 구간 합은 24가 된다.
4. 느리게 갱신되는 세그먼트 트리의 구조와 코드 예시
기본 세그먼트 트리와의 차이점
기본 세그먼트 트리는 리프 노드에 배열 값을 저장하고, 부모 노드는 자식들의 구간 합을 저장한다. 느리게 갱신되는 세그먼트 트리는 여기게 lazy 배열을 추가해 지연된 업데이트를 기록한다. 아래 코드는 https://www.acmicpc.net/problem/10999 의 정답 코드이다.
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
typedef long long ll;
vector<ll> tree, lazy;
int n;
// 세그먼트 트리 초기화
void init(vector<ll>& arr, int s, int e, int node) {
if (s == e) {
tree[node] = arr[s];
} else {
int mid = (s + e) / 2;
init(arr, s, mid, node * 2);
init(arr, mid + 1, e, node * 2 + 1);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
}
// Lazy 값을 트리에 반영
void update_lazy(int s, int e, int node) {
if (lazy[node] != 0) {
tree[node] += (e - s + 1) * lazy[node];
if (s != e) {
lazy[node * 2] += lazy[node];
lazy[node * 2 + 1] += lazy[node];
}
lazy[node] = 0;
}
}
// 구간 업데이트
void update_range(int s, int e, int l, int r, int node, ll val) {
update_lazy(s, e, node); // lazy 값을 먼저 반영
if (e < l || s > r) return; // 구간 벗어남
if (s >= l && e <= r) { // 구간이 완전히 포함된 경우
tree[node] += (e - s + 1) * val;
if (s != e) {
lazy[node * 2] += val;
lazy[node * 2 + 1] += val;
}
return;
}
int mid = (s + e) / 2;
update_range(s, mid, l, r, node * 2, val);
update_range(mid + 1, e, l, r, node * 2 + 1, val);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
// 구간 합 구하기
// 기존 세그먼트 트리는 idx를 이용했지만
// 느리게 갱신되는 세그먼트 트리는 구간을 이용
ll query(int s, int e, int l, int r, int node) {
update_lazy(s, e, node); // lazy 값을 먼저 반영
if (e < l || s > r) return 0; // 구간 벗어남
if (s >= l && e <= r) return tree[node]; // 구간이 완전히 포함된 경우
int mid = (s + e) / 2;
ll left = query(s, mid, l, r, node * 2);
ll right = query(mid + 1, e, l, r, node * 2 + 1);
return left + right;
}
int main() {
int m, k;
cin >> n >> m >> k;
vector<ll> arr(n);
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
int h = (int)ceil(log2(n));
int tree_size = (1 << (h + 1));
tree.resize(tree_size);
lazy.resize(tree_size);
init(arr, 0, n - 1, 1);
for (int i = 0; i < m + k; i++) {
int a;
cin >> a;
if (a == 1) {
int b, c;
ll d;
cin >> b >> c >> d;
update_range(0, n - 1, b - 1, c - 1, 1, d);
} else if (a == 2) {
int b, c;
cin >> b >> c;
cout << query(0, n - 1, b - 1, c - 1, 1) << '\n';
}
}
return 0;
}
'자료구조 및 알고리즘' 카테고리의 다른 글
| [자료구조 및 알고리즘] 펜윅트리 (Fenwick Tree, Binary Indexed Tree) (4) | 2024.11.02 |
|---|---|
| [자료구조 및 알고리즘] 그래프에서 음의 사이클 구하기 (벨만 포드 알고리즘, 플로이드 워셜 알고리즘) (0) | 2024.11.02 |
| [자료구조 및 알고리즘] 세그먼트 트리 (4) | 2024.10.18 |
| [자료구조 및 알고리즘] 비트마스킹 (bit masking) (0) | 2024.08.13 |
| [자료구조 및 알고리즘] 배낭 문제와 그 변형 (0) | 2024.08.13 |
느리게 갱신되는 세그먼트 트리 (Lazy Propagation)
느리게 갱신되는 세그먼트 트리(Lazy Propagation)는 세그먼트 트리에서 구간 업데이트를 더 효율적으로 처리하기 위해 사용하는 기법이다. 구간의 여러 값을 한 번에 갱신하고, 그 후에 구간에 대한 정보를 빠르게 얻어야 할 때 사용된다.
1. 느리게 갱신되는 세그먼트 트리란?
기본 세그먼트 트리는 특정 구간의 값(합, 최대값 등)을 빠르게 쿼리할 수 있게 해준다. 그런데 만약 구간 내 모든 값에 동일한 연산(ex. 더하기)을 여러 번 적용해야 하는 경우, 기본 세그먼트 트리로는 비효율적일 수 있다. 최악의 경우 nlogn의 시간이 걸릴 수 있기 때문이다. 이때 느리게 갱신되는 세그먼트 트리를 사용하면 구간 전체에 대한 업데이트를 지연시키고 나중에 한꺼번에 처리할 수 있다.
이를테면, 배열 [1, 2, 3, 4, 5] 가 있다. 그리고 3번째에서 5번째까지 모든 값에 2를 더하는 작업을 한다면, 기본 세그먼트 트리에서는 매번 그 범위의 값을 전부 순회하면서 하나씩 더해줘야 한다. 이런 작업이 반복되면 비효율적일 것이다.
느리게 갱신되는 세그먼트 트리는 이런 작업을 즉시 처리하지 않고 지연시켜 두었다가 필요할 때 한꺼번에 처리한다. 이렇게 하면 불필요한 계산을 줄요 효율적으로 구간 업데이트를 처리할 수 있다.
2. 어떤 경우에 사용하는지
느리게 갱신되는 세그먼트 트리는 구간 전체에 대해 일괄적인 업데이트가 자주 발생하는 경우에 사용해야 한다.
- 구간 내 모든 값에 더하기/빼기와 같은 연산을 적용하는 경우
- 대규모 배열에서 구간 내 값들을 일일이 업데이트하는 대신 한꺼번에 처리하고자 할 때
이처럼 여러 값에 대해 동일한 작업을 반복해야 할 때, 느리게 갱신되는 세그먼트 트리는 업데이트와 쿼리를 모두 효율적으로 처리할 수 있다.
3. 느리게 갱신되는 세그먼트 트리의 작동 원리
기본 세그먼트 트리에서는 값이 변경될 때 바로 트리의 모든 관련 노드에 반영한다. 하지만 느리게 갱신되는 세그먼트 트리에서는 lazy 배열을 사용해 변경 사항을 나중에 한꺼번에 반영한다. 이 방법으로 필요할 때만 값을 갱신해 시간을 절약한다.
작동순서
- 구간 업데이트 요청이 들어오면, 해당 구간에 대한 업데이트를 즉시 처리하지 않고 lazy 배열에 변경 사항을 저장해 둔다.
- 그 후 해당 구간에 쿼리 요청이 들어오면, 그때 lazy 배열에 저장된 값을 트리에 반영하여 한꺼번에 처리한다.
- 이 과정을 통해 구간 업데이트를 지연시키고 나중에 필요할 때만 한 번에 갱신하므로, 시간 복잡도를 줄일 수 있다.
예시 상황
- 배열: [1, 2, 3, 4, 5]
- 트리를 초기화하고 나면 이 배열을 세그먼트 트리로 변환해서 관리한다.
- 2번째부터 4번째 값에 3을 더하는 작업을 한다고 가정
- 그 후 1번째부터 5번째 값의 합을 구하는 쿼리를 처리
1. 초기 상태
초기 배열은 [1, 2, 3, 4, 5]이다. 세그먼트 트리는 다음과 같이 초기화된다. 트리 구조에서는 부모 노드가 자식 노드들의 합을 가지고 있다.

- 루트 노드 15는 전체 배열의 합인 1 + 2 + 3 + 4 + 5 = 15이다.
- 각 리프 노드는 배열의 개별 값을 나타낸다.
2. 구간 업데이트 요청 (2번째부터 4번째까지의 값에 3을 더하기)
이제 2번째부터 4번째 값에 3을 더하는 작업이 들어온다. 이때 트리 전체를 바로 갱신하지 않고 lazy propagation을 이용해 lazy 배열에 값을 저장해서 나중에 처리한다.
- 2번째부터 4번째 구간을 포함하는 노드들의 lazy 값을 업데이트한다.
- 즉, 구간을 나누어 담당하는 노드들에 대해 "나중에 이 값에 3을 더하겠다"는 정보를 lazy 배열에 저장한다.

3. 구간 합 쿼리 요청 (1번째부터 5번째까지의 합 구하기)
이제 1번째부터 5번째 구간 합을 구하는 쿼리가 들어온다. 이때 쿼리 전에, lazy 배열에 저장된 값을 트리에 반영한다.
- 루트 노드로부터 시작해 트리를 내려가면서 lazy 값을 적용한다.
- [2, 4] 구간에 3을 더하라는 지연된 작업이 있으므로 이를 적용한 후 쿼리를 처리한다.
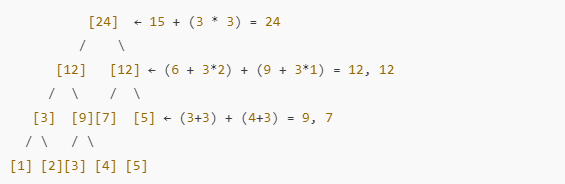
- lazy 값을 반영: 2번째부터 4번째 구간에 각각 3을 더해야 하므로, [2,4] 구간에 해당하는 노드들에 대해 3을 더한 후 트리 값을 업데이트한다.
- 쿼리 처리: lazy 값이 반영된 후, 최종 구간 합은 24가 된다.
4. 느리게 갱신되는 세그먼트 트리의 구조와 코드 예시
기본 세그먼트 트리와의 차이점
기본 세그먼트 트리는 리프 노드에 배열 값을 저장하고, 부모 노드는 자식들의 구간 합을 저장한다. 느리게 갱신되는 세그먼트 트리는 여기게 lazy 배열을 추가해 지연된 업데이트를 기록한다. 아래 코드는 https://www.acmicpc.net/problem/10999 의 정답 코드이다.
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
typedef long long ll;
vector<ll> tree, lazy;
int n;
// 세그먼트 트리 초기화
void init(vector<ll>& arr, int s, int e, int node) {
if (s == e) {
tree[node] = arr[s];
} else {
int mid = (s + e) / 2;
init(arr, s, mid, node * 2);
init(arr, mid + 1, e, node * 2 + 1);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
}
// Lazy 값을 트리에 반영
void update_lazy(int s, int e, int node) {
if (lazy[node] != 0) {
tree[node] += (e - s + 1) * lazy[node];
if (s != e) {
lazy[node * 2] += lazy[node];
lazy[node * 2 + 1] += lazy[node];
}
lazy[node] = 0;
}
}
// 구간 업데이트
void update_range(int s, int e, int l, int r, int node, ll val) {
update_lazy(s, e, node); // lazy 값을 먼저 반영
if (e < l || s > r) return; // 구간 벗어남
if (s >= l && e <= r) { // 구간이 완전히 포함된 경우
tree[node] += (e - s + 1) * val;
if (s != e) {
lazy[node * 2] += val;
lazy[node * 2 + 1] += val;
}
return;
}
int mid = (s + e) / 2;
update_range(s, mid, l, r, node * 2, val);
update_range(mid + 1, e, l, r, node * 2 + 1, val);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
// 구간 합 구하기
// 기존 세그먼트 트리는 idx를 이용했지만
// 느리게 갱신되는 세그먼트 트리는 구간을 이용
ll query(int s, int e, int l, int r, int node) {
update_lazy(s, e, node); // lazy 값을 먼저 반영
if (e < l || s > r) return 0; // 구간 벗어남
if (s >= l && e <= r) return tree[node]; // 구간이 완전히 포함된 경우
int mid = (s + e) / 2;
ll left = query(s, mid, l, r, node * 2);
ll right = query(mid + 1, e, l, r, node * 2 + 1);
return left + right;
}
int main() {
int m, k;
cin >> n >> m >> k;
vector<ll> arr(n);
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
int h = (int)ceil(log2(n));
int tree_size = (1 << (h + 1));
tree.resize(tree_size);
lazy.resize(tree_size);
init(arr, 0, n - 1, 1);
for (int i = 0; i < m + k; i++) {
int a;
cin >> a;
if (a == 1) {
int b, c;
ll d;
cin >> b >> c >> d;
update_range(0, n - 1, b - 1, c - 1, 1, d);
} else if (a == 2) {
int b, c;
cin >> b >> c;
cout << query(0, n - 1, b - 1, c - 1, 1) << '\n';
}
}
return 0;
}
'자료구조 및 알고리즘' 카테고리의 다른 글
| [자료구조 및 알고리즘] 펜윅트리 (Fenwick Tree, Binary Indexed Tree) (4) | 2024.11.02 |
|---|---|
| [자료구조 및 알고리즘] 그래프에서 음의 사이클 구하기 (벨만 포드 알고리즘, 플로이드 워셜 알고리즘) (0) | 2024.11.02 |
| [자료구조 및 알고리즘] 세그먼트 트리 (4) | 2024.10.18 |
| [자료구조 및 알고리즘] 비트마스킹 (bit masking) (0) | 2024.08.13 |
| [자료구조 및 알고리즘] 배낭 문제와 그 변형 (0) | 2024.08.13 |
