오일러 경로 테크닉
오일러 경로 테크닉에서는 DFS(깊이 우선 탐색)을 사용하여 그래프를 순회하면서 특정 정보(노드 방문 순서, 간선 순회 순서 등)를 기록한다. 일반적으로 오일러 투어라고도 불리며, 트리나 그래프의 정보를 flat한 배열 형태로 변환한다. 세그먼트 트리 같은 자료구조에서 효율적으로 처리할 수 있도록 한다. 트리의 dfs 순회를 기반으로 각 노드의 방문 순서 또는 진입/퇴장 시간을 기록한 배열을 생성한다.
세그먼트 트리는 일반적으로 배열을 대상으로 작동하는데, 오일러 경로 테크닉을 사용하면 트리 문제를 배열 문제로 변환하여 세그먼트 트리에서 구간 합, 구간 최대/최소값 쿼리 또는 특정 노드와 서브트리에 대한 작업을 효율적으로 수행할 수 있다.
예시
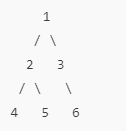
위와 같은 트리구조가 있다. ETT를 사용하면 다음과 같이 방문순서가 기록된다.
DFS 순서: [1, 2, 4, 5, 3, 6]
In-Time: [1, 2, 3, 4, 5, 6]
Out-Time: [6, 5, 3, 4, 6, 6]
ETT 배열은 다음과 같다
ETT 배열: [1, 2, 4, 5, 3, 6]코드
코드는 간단하다. 시작 배열과 도착 배열, cnt 변수 1개와 dfs 함수 하나면 구현할 수 있다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int MAX_N = 100003;
int s[MAX_N], e[MAX_N], cnt;
vector<int> adj[MAX_N];
void dfs(int x, int par) {
s[x] = ++cnt;
for (int i : adj[x]) {
if (i != par) {
dfs(i, x);
}
}
e[x] = cnt;
}
'자료구조 및 알고리즘' 카테고리의 다른 글
| [자료구조 및 알고리즘] unordered_map과 배열의 성능 차이 (0) | 2024.12.01 |
|---|---|
| [자료구조 및 알고리즘] 머지소트트리 (merge sort tree) (0) | 2024.11.27 |
| [자료구조 및 알고리즘] 강한 연결 요소 (Strongly Connected Component, SCC) (0) | 2024.11.15 |
| [자료구조 및 알고리즘] 펜윅트리 (Fenwick Tree, Binary Indexed Tree) (4) | 2024.11.02 |
| [자료구조 및 알고리즘] 그래프에서 음의 사이클 구하기 (벨만 포드 알고리즘, 플로이드 워셜 알고리즘) (0) | 2024.11.02 |
