강한 연결 요소 (Strongly Connected Component, SCC)
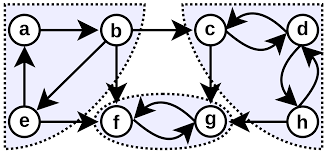
강한 연결 요소(SCC)란 방향 그래프에서 어떤 두 점 u와 v가 있을 때 u -> v와 v -> u 두 방향으로 모두 경로가 존재하는 정점들의 최대 집합을 의미한다.
특징
- SCC는 방향 그래프의 구성 요소
- 무방향 그래프에서의 연결 요소와 비슷하지만, 방향성이 존재하는 그래프에서 정의된다.
- SCC 내의 모든 정점은 서로 도달 가능해야 한다.
- DAG로 변환 가능
- 모든 SCC를 하나의 정점으로 압축하면 방향성이 없는 비순환 그래프 (DAG, Directed Acyclic Graph)가 만들어진다.
- 이 DAG는 SCC의 상호 연결 관계를 보여준다.
- 응용
- SCC는 그래프 분석, 순환 검출, 도미노 문제, 인터넷 네트워크 분석, 강한 결합성을 가진 시스템 찾기 등 다양한 분야에서 활용된다.
SCC를 찾는 알고리즘
SCC를 찾는 알고리즘은 2가지가 있다.
1. 코사라주(Kosaraju) 알고리즘
코사라주 알고리즘은 두 번의 DFS를 사용하여 SCC를 찾는다.
- 첫 번째 DFS
- 각 정점의 종료 시간을 기준으로 정렬한다.
- 전치 그래프(Transpose Graph) 생성
- 모든 간선을 뒤집어 새로운 전치 그래프를 만든다.
- 두 번째 DFS
- 종료 시간이 늦은 정점부터 전치 그래프에서 DFS를 수행하며 SCC를 찾는다.
시간복잡도: O(V + E)
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
const int MAX_N = 100003;
vector<int> adj[MAX_N], rev_adj[MAX_N];
stack<int> stk;
bool visited[MAX_N];
vector<vector<int>> scc;
void dfs1(int node) {
visited[node] = true;
for (int neighbor : adj[node]) {
if (!visited[neighbor]) {
dfs1(neighbor);
}
}
stk.push(node);
}
void dfs2(int node, vector<int>& component) {
visited[node] = true;
component.push_back(node);
for (int neighbor : rev_adj[node]) {
if (!visited[neighbor]) {
dfs2(neighbor, component);
}
}
}
void kosaraju(int n) {
// Step 1: Perform the first DFS to fill the stack
for (int i = 1; i <= n; i++) {
if (!visited[i]) {
dfs1(i);
}
}
// Step 2: Transpose the graph
for (int u = 1; u <= n; u++) {
for (int v : adj[u]) {
rev_adj[v].push_back(u);
}
}
// Step 3: Perform the second DFS in the order of the stack
fill(visited, visited + n + 1, false);
while (!stk.empty()) {
int node = stk.top();
stk.pop();
if (!visited[node]) {
vector<int> component;
dfs2(node, component);
scc.push_back(component);
}
}
}
int main() {
int n, m;
cin >> n >> m;
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
adj[u].push_back(v);
}
kosaraju(n);
// Output SCCs
cout << "Number of SCCs: " << scc.size() << '\n';
for (const auto& component : scc) {
for (int node : component) {
cout << node << " ";
}
cout << '\n';
}
return 0;
}
2. 타잔(Tarjan) 알고리즘
타잔 알고리즘은 DFS를 1번만 사용하여 SCC를 찾는다.
- DFS 방문 순서 기록
- 각 정점의 방문 순서와 최소 도달 가능한 방문 순서를 기록
- 스택으로 SCC 관리
- 현재 탐색 중인 SCC에 속한 정점들을 스택에 저장한다.
- SCC 탐색 종료 조건
- DFS 탐색 도중, 현재 정점이 SCC의 루트라면 스택에서 정점들을 꺼내 새로운 SCC를 구성한다.
시간복잡도: O(V + E)
#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>
using namespace std;
const int MAX_N = 100003;
vector<int> adj[MAX_N];
int ids[MAX_N], low[MAX_N];
bool on_stack[MAX_N];
stack<int> stk;
vector<vector<int>> scc;
int id, scc_count;
void tarjanDFS(int node) {
ids[node] = low[node] = ++id;
stk.push(node);
on_stack[node] = true;
for (int neighbor : adj[node]) {
if (ids[neighbor] == 0) { // If neighbor is not visited
tarjanDFS(neighbor);
low[node] = min(low[node], low[neighbor]);
} else if (on_stack[neighbor]) { // If neighbor is in the stack
low[node] = min(low[node], ids[neighbor]);
}
}
// If node is a root of an SCC
if (ids[node] == low[node]) {
vector<int> component;
while (true) {
int top = stk.top();
stk.pop();
on_stack[top] = false;
component.push_back(top);
if (top == node) break;
}
scc.push_back(component);
}
}
void tarjan(int n) {
id = 0;
fill(ids, ids + n + 1, 0);
fill(low, low + n + 1, 0);
fill(on_stack, on_stack + n + 1, false);
for (int i = 1; i <= n; i++) {
if (ids[i] == 0) {
tarjanDFS(i);
}
}
}
int main() {
int n, m;
cin >> n >> m;
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
adj[u].push_back(v);
}
tarjan(n);
// Output SCCs
cout << "Number of SCCs: " << scc.size() << '\n';
for (const auto& component : scc) {
for (int node : component) {
cout << node << " ";
}
cout << '\n';
}
return 0;
}
SCC vs 일반 연결 요소
| 특징 | 일반 연결 요소 | SCC |
| 그래프 종류 | 무방향 그래프 | 방향 그래프 |
| 정점 간 연결성 | 두 정점 사이에 경로가 존재 | 두 정점 사이에 양방향 경로가 존재 |
| 구성 | 그래프의 연결된 하위 그래프 | 그래프의 강하게 연결된 하위 그래프 |
| 알고리즘 | DFS/ BFS | Kosaraju, Tarjan |
Tarjan vs Kosaraju
- 코사라주 알고리즘은 구현이 직관적이며 문제를 단계별로 접근하기 좋다.
- 타잔 알고리즘은 메모리에 효율적이며, 특히 SCC를 실시간으로 구성해야 할 때 유리하다.
'자료구조 및 알고리즘' 카테고리의 다른 글
| [자료구조 및 알고리즘] 머지소트트리 (merge sort tree) (0) | 2024.11.27 |
|---|---|
| [자료구조 및 알고리즘] 오일러 경로 테크닉 (1) | 2024.11.27 |
| [자료구조 및 알고리즘] 펜윅트리 (Fenwick Tree, Binary Indexed Tree) (4) | 2024.11.02 |
| [자료구조 및 알고리즘] 그래프에서 음의 사이클 구하기 (벨만 포드 알고리즘, 플로이드 워셜 알고리즘) (0) | 2024.11.02 |
| [자료구조 및 알고리즘] 느리게 갱신되는 세그먼트 트리 (Lazy Propagation) (2) | 2024.10.18 |
