Heap
1. 힙은 완전이진트리를 기본으로한 자료구조로, O(logN)의 시간복잡도를 가지고 있다.
2. 여러 개의 값 중 최대값, 최소값을 빠르게 찾아내도록 만들어진 자료구조이다. 우선순위 큐 구현 시에 사용한다.
3. 힙은 반정렬 상태(느슨한 정렬 상태)를 유지한다. 이를테면 최소힙일 때, 작은 값이 상위 레벨에 있고 큰 값이 하위 레벨에 있다는 정도.
4. 힙 트리에서는 중복된 값을 허용한다. (이진 탐색 트리에서는 중복된 값을 허용하지 않는다.)
힙의 종류
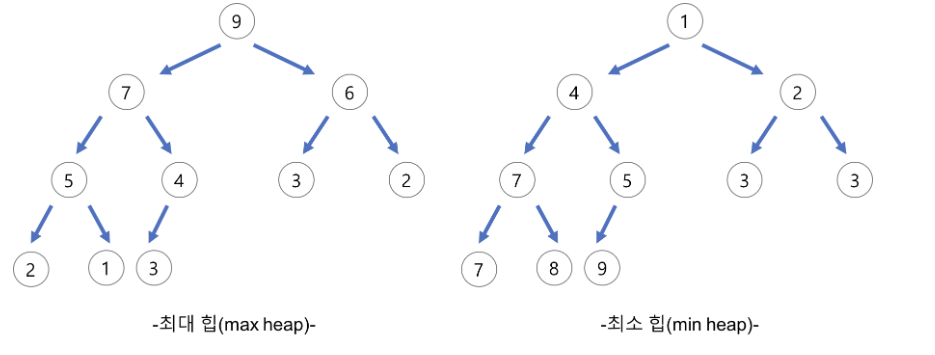
최대힙
부모노드의 키 값이 자식노드의 키값보다 항상 크거나 같 힙. 최대 힙에서는 루트 노드에 이는 값이 제일 크므로 최대값을 찾는데 소요되는 연산의 시간복잡도는 O(1)이다. 그리고 완전 이진 트리이기 때문에 배열을 사용하여 효율적으로 관리할 수 있다.
최소힙
부모노드의 값이 자식노드의 값보다 항상 작거나 같은 힙. 값의 대소관계는 부모 자식 간에만 성립하고 형제간에는 성립하지 않는다.
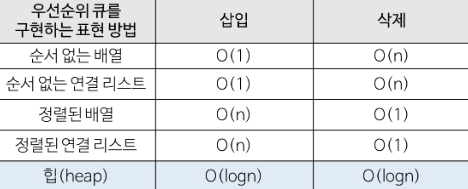
우선순위 큐의 구현에 있어서 힙을 사용하는 것이 가장 효율적이라고 한다.
힙의 구현
1. 힙을 저장하는 표준적인 자료구조는 배열이다.
2. 구현을 쉽게 하기 위해 배열의 첫번째 인덱스인 0은 사용하지 않는다고 한다.
3. 특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않는다. (ex 루트 노드 1의 오른쪽 노드 번호는 항상 3)
부모 노드와 자식노드의 관계
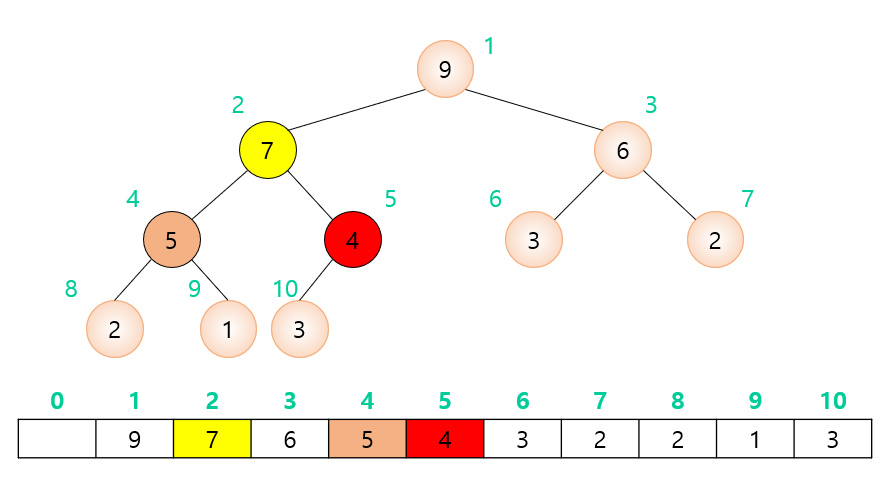
왼쪽 자식 index = (부모 index) * 2
오른쪽 자식 index = (부모 index) * 2 + 1
부모 index = (자식 index) / 2
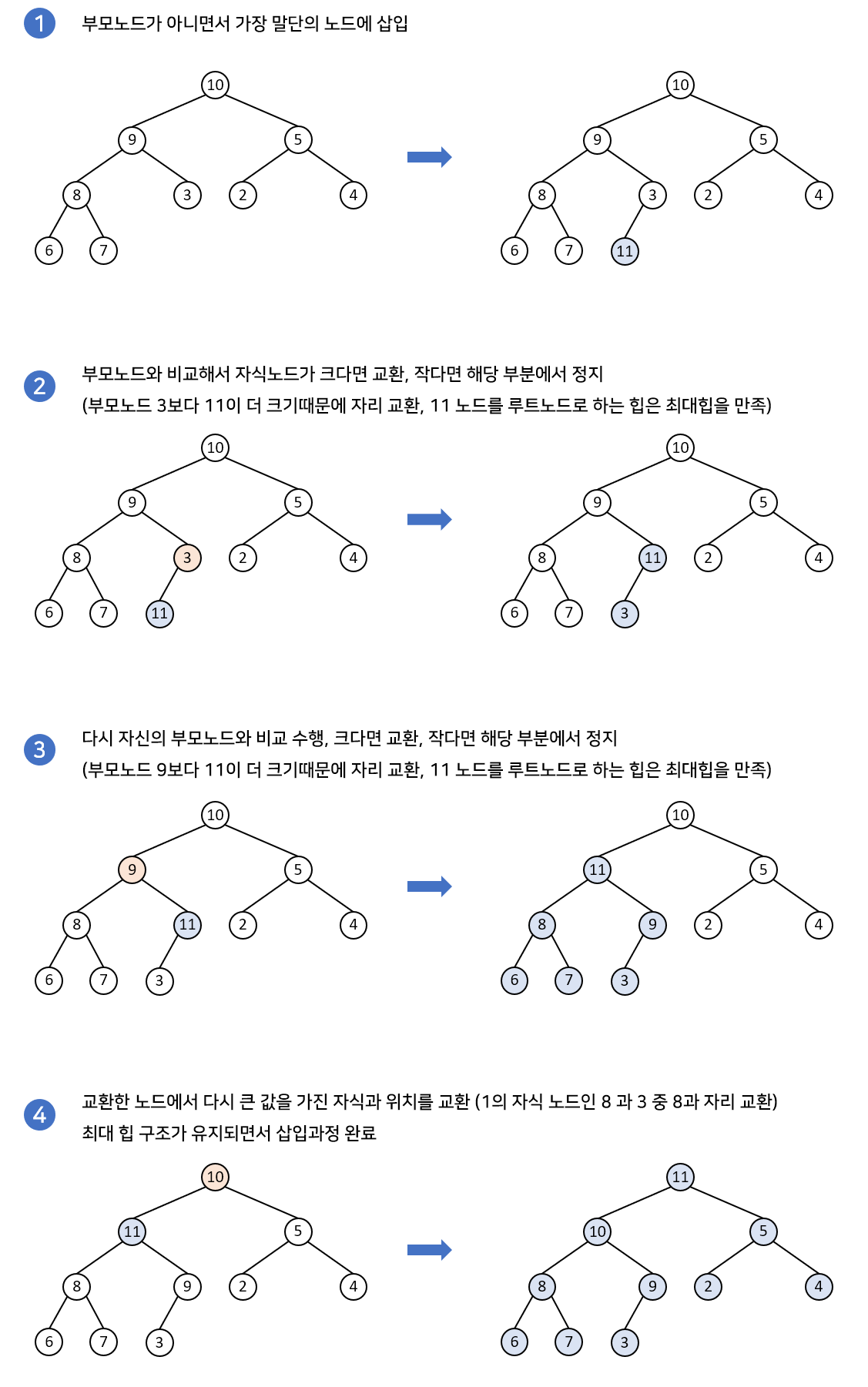
힙의 삽입
1. 힙에 새로운 요소가 들어오면, 새로운 노드를 힙의 마지막 노드에 삽입한다.
2. 새로운 노드를 부모 노드들과 교환환다.
void insert_max_heap(int x) {
maxHeap[++heapSize] = x; // 힙 크기 하나 증가, 마지막 노드에 x 추가
for( int i = heapSize; i > 1; i /= 2) {
// 마지막 노드가 자신의 부모 노드보다 크면 swap
if(maxHeap[i/2] < maxHeap[i]) {
swap(i/2, i);
} else {
break;
}
}
}
힙의 삭제
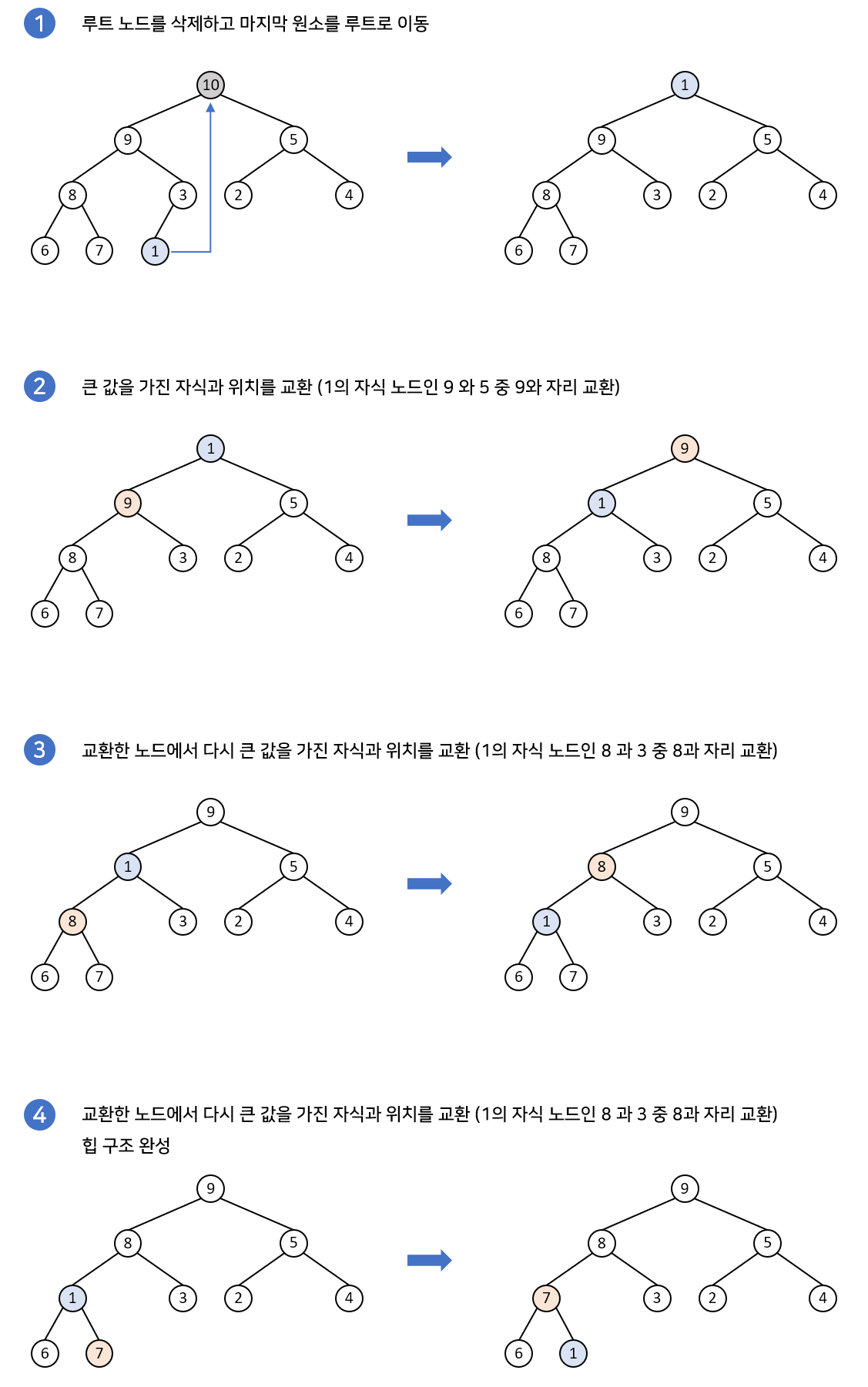
1. 최대 힙에서 최대값은 루트 노드이므로 루트노드가 삭제된다. (최대 힙에서 삭제 연산은 최대값 요소를 삭제하는 것)
2. 삭제된 루트 노드에는 힙의 마지막 노드를 가져온다.
3. 힙을 재구성한다. 자식노드가 더 이상 없거나 자식보다 클 경우 재구성 종료.
// 최대 힙 삭제
int delete_max_heap() {
if(heapSize == 0) // 배열이 비어있으면 리턴
return 0;
int item = maxHeap[1]; // 루트 노드의 값을 저장
maxHeap[1] = maxHeap[heapSize]; // 마지막 노드 값을 루트로 이동
maxHeap[heapSize--] = 0; // 힙 크기를 하나 줄이고 마지막 노드 0 초기화
for(int i = 1; i*2 <= heapSize;) {
// 마지막 노드가 왼쪽 노드와 오른쪽 노드보다 크면 끝
if(maxHeap[i] > maxHeap[i*2] && maxHeap[i] > maxHeap[i*2+1]) {
break;
}
// 왼쪽 노드가 더 큰 경우, swap
else if (maxHeap[i*2] > maxHeap[i*2+1]) {
swap(i, i*2);
i = i*2;
}
// 오른쪽 노드가 더 큰 경우, swap
else {
swap(i, i*2+1);
i = i*2+1;
}
}
return item;
}
'자료구조 및 알고리즘' 카테고리의 다른 글
| [자료구조 및 알고리즘] 0-1 너비우선탐색 (0-1 BFS) (1) | 2023.11.24 |
|---|---|
| [자료구조 및 알고리즘] 다익스트라 알고리즘 (Dijkstra Algorithm) (0) | 2023.11.24 |
| [자료구조 및 알고리즘] 파라메트릭 서치 (Parametric Search) (0) | 2023.09.05 |
| [자료구조 및 알고리즘] 이진탐색 (Binary Search) (0) | 2023.08.30 |
| [자료구조 및 알고리즘] 계수정렬(Counting Sort) (0) | 2023.07.19 |
Heap
1. 힙은 완전이진트리를 기본으로한 자료구조로, O(logN)의 시간복잡도를 가지고 있다.
2. 여러 개의 값 중 최대값, 최소값을 빠르게 찾아내도록 만들어진 자료구조이다. 우선순위 큐 구현 시에 사용한다.
3. 힙은 반정렬 상태(느슨한 정렬 상태)를 유지한다. 이를테면 최소힙일 때, 작은 값이 상위 레벨에 있고 큰 값이 하위 레벨에 있다는 정도.
4. 힙 트리에서는 중복된 값을 허용한다. (이진 탐색 트리에서는 중복된 값을 허용하지 않는다.)
힙의 종류
최대힙
부모노드의 키 값이 자식노드의 키값보다 항상 크거나 같 힙. 최대 힙에서는 루트 노드에 이는 값이 제일 크므로 최대값을 찾는데 소요되는 연산의 시간복잡도는 O(1)이다. 그리고 완전 이진 트리이기 때문에 배열을 사용하여 효율적으로 관리할 수 있다.
최소힙
부모노드의 값이 자식노드의 값보다 항상 작거나 같은 힙. 값의 대소관계는 부모 자식 간에만 성립하고 형제간에는 성립하지 않는다.

우선순위 큐의 구현에 있어서 힙을 사용하는 것이 가장 효율적이라고 한다.

힙의 구현
1. 힙을 저장하는 표준적인 자료구조는 배열이다.
2. 구현을 쉽게 하기 위해 배열의 첫번째 인덱스인 0은 사용하지 않는다고 한다.
3. 특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않는다. (ex 루트 노드 1의 오른쪽 노드 번호는 항상 3)
부모 노드와 자식노드의 관계

왼쪽 자식 index = (부모 index) * 2
오른쪽 자식 index = (부모 index) * 2 + 1
부모 index = (자식 index) / 2
힙의 삽입
1. 힙에 새로운 요소가 들어오면, 새로운 노드를 힙의 마지막 노드에 삽입한다.
2. 새로운 노드를 부모 노드들과 교환환다.

void insert_max_heap(int x) {
maxHeap[++heapSize] = x; // 힙 크기 하나 증가, 마지막 노드에 x 추가
for( int i = heapSize; i > 1; i /= 2) {
// 마지막 노드가 자신의 부모 노드보다 크면 swap
if(maxHeap[i/2] < maxHeap[i]) {
swap(i/2, i);
} else {
break;
}
}
}
힙의 삭제
1. 최대 힙에서 최대값은 루트 노드이므로 루트노드가 삭제된다. (최대 힙에서 삭제 연산은 최대값 요소를 삭제하는 것)
2. 삭제된 루트 노드에는 힙의 마지막 노드를 가져온다.
3. 힙을 재구성한다. 자식노드가 더 이상 없거나 자식보다 클 경우 재구성 종료.

// 최대 힙 삭제
int delete_max_heap() {
if(heapSize == 0) // 배열이 비어있으면 리턴
return 0;
int item = maxHeap[1]; // 루트 노드의 값을 저장
maxHeap[1] = maxHeap[heapSize]; // 마지막 노드 값을 루트로 이동
maxHeap[heapSize--] = 0; // 힙 크기를 하나 줄이고 마지막 노드 0 초기화
for(int i = 1; i*2 <= heapSize;) {
// 마지막 노드가 왼쪽 노드와 오른쪽 노드보다 크면 끝
if(maxHeap[i] > maxHeap[i*2] && maxHeap[i] > maxHeap[i*2+1]) {
break;
}
// 왼쪽 노드가 더 큰 경우, swap
else if (maxHeap[i*2] > maxHeap[i*2+1]) {
swap(i, i*2);
i = i*2;
}
// 오른쪽 노드가 더 큰 경우, swap
else {
swap(i, i*2+1);
i = i*2+1;
}
}
return item;
}
'자료구조 및 알고리즘' 카테고리의 다른 글
| [자료구조 및 알고리즘] 0-1 너비우선탐색 (0-1 BFS) (1) | 2023.11.24 |
|---|---|
| [자료구조 및 알고리즘] 다익스트라 알고리즘 (Dijkstra Algorithm) (0) | 2023.11.24 |
| [자료구조 및 알고리즘] 파라메트릭 서치 (Parametric Search) (0) | 2023.09.05 |
| [자료구조 및 알고리즘] 이진탐색 (Binary Search) (0) | 2023.08.30 |
| [자료구조 및 알고리즘] 계수정렬(Counting Sort) (0) | 2023.07.19 |
