트리
트리는 그래프의 일종으로 노드들이 나무 가지처럼 연결된 비선형 계층적 자료구조이다.
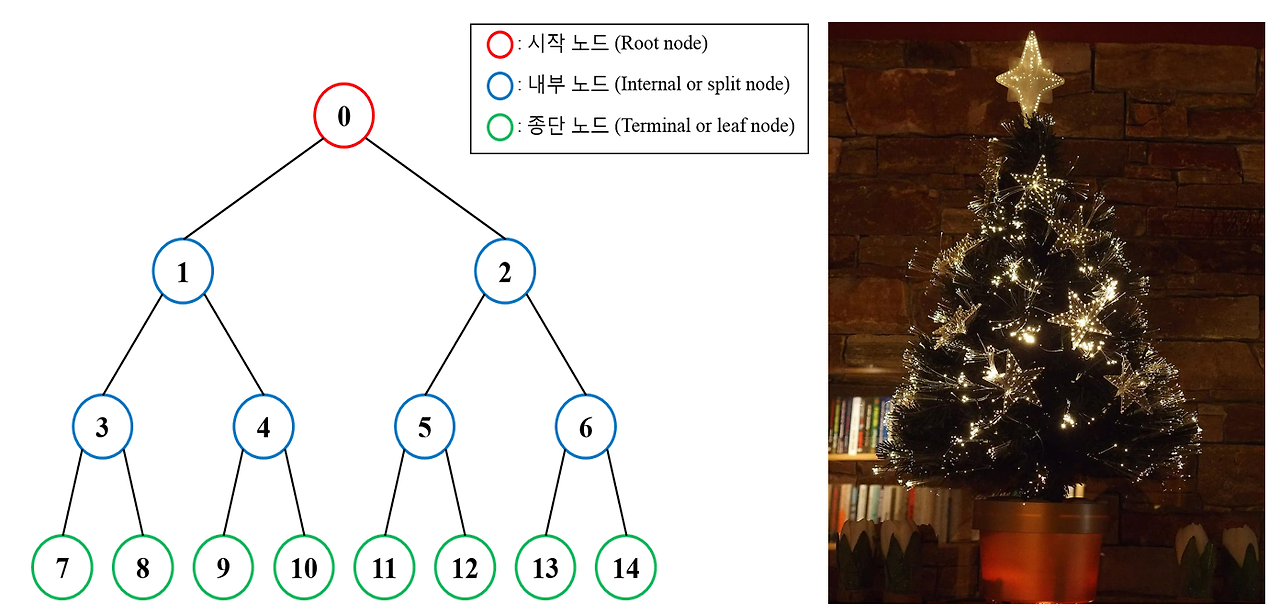
트리 용어
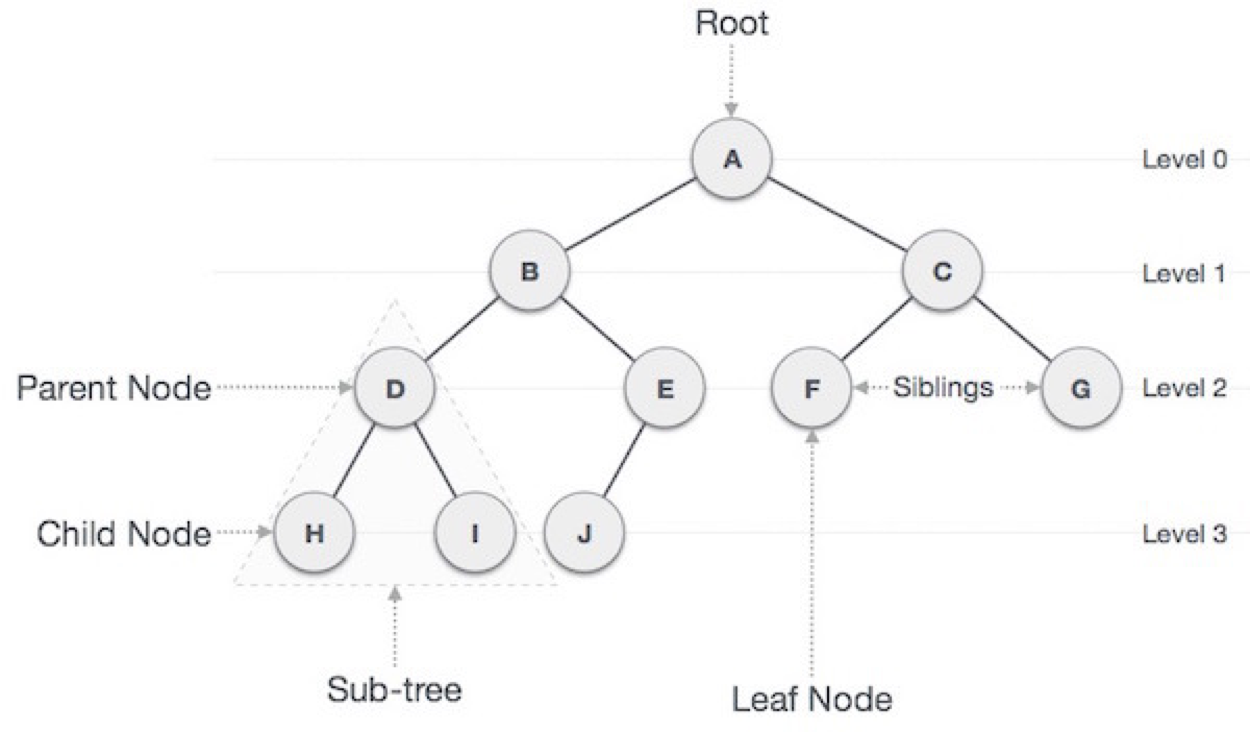
- Node: 트리 구조의 교점으로 node는 데이터를 가지고 있고, 자식 노드를 가질 수 있음.
- Root Node: 트리 구조에서 가장 위에 있는 노드. 즉, 트리의 시작점이 되는 노드.
- Edge: 트리를 구성하기 위해 노드와 노드를 연결하는 선.
- Level: 트리의 특정 깊이를 가지는 노드의 집합.
- Degree: 각 노드가 가진 가지의 수. '차수'라고도 함
- Leaf Node (Terminal Node): 하위에 다른 노드가 연결되어 있지 않은 노드.
- Internal Node: Leaf Node를 제외한, 중간에 위치한 노드들.

트리의 특징
- 트리 자료구조는 일반적으로 대상 정보의 각 항목들을 계층적으로 구조화할 때 사용하는 비선형 자료구조
- Tree 구조는 데이터의 저장의 의미보다는 저장된 데이터를 더 효과적으로 탐색하기 위해 사용
- 리스트와 다르게 데이터가 단순히 나열되는 구조가 아니라, 부모와 자식의 계층적인 관계로 표현
- 트리는 그래프의 한 종류이며 사이클이 없음
- 트리에서 Root Node를 제외한 모든 노드는 단 하나의 부모노드를 가진다.
트리 순회
트리의 순회란 트리의 각 노드를 체계적인 방법으로 탐색하는 과정을 말한다. 노드를 탐색하는 순서에 따라 전위 순회, 중위 순회, 후위 순회 세 가지로 나뉜다.
1) 전위 순회(preorder)
- 루트노드 -> 왼쪽 서브 트리 -> 오른쪽 서브트리 순으로 순회하는 방식
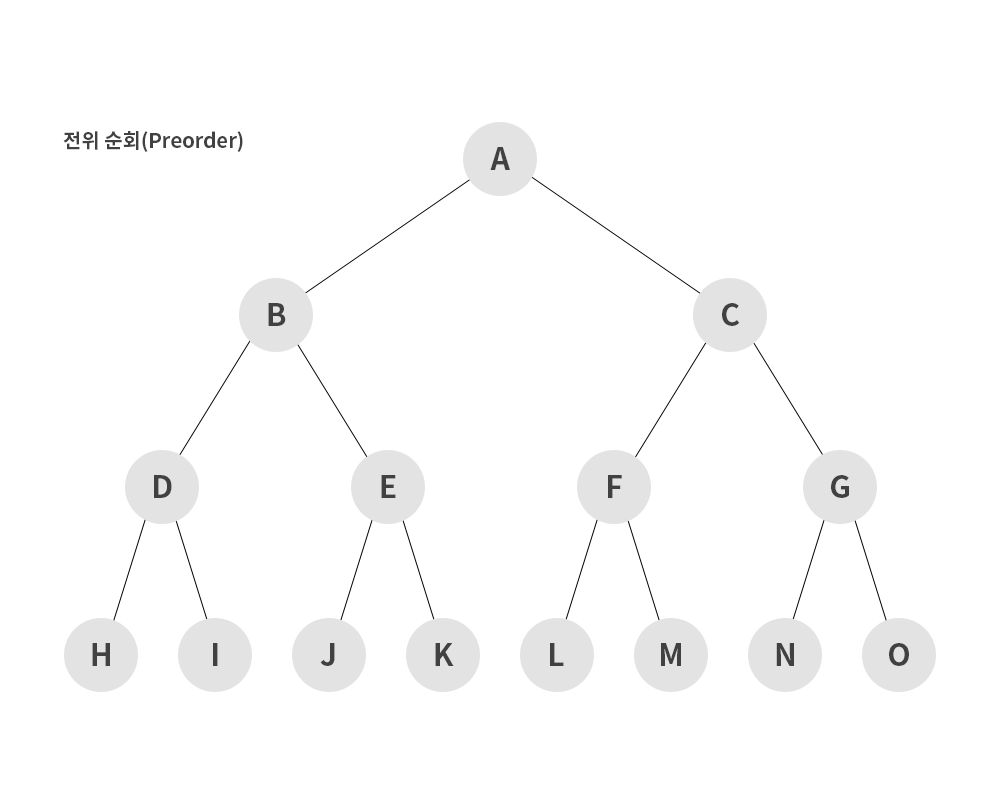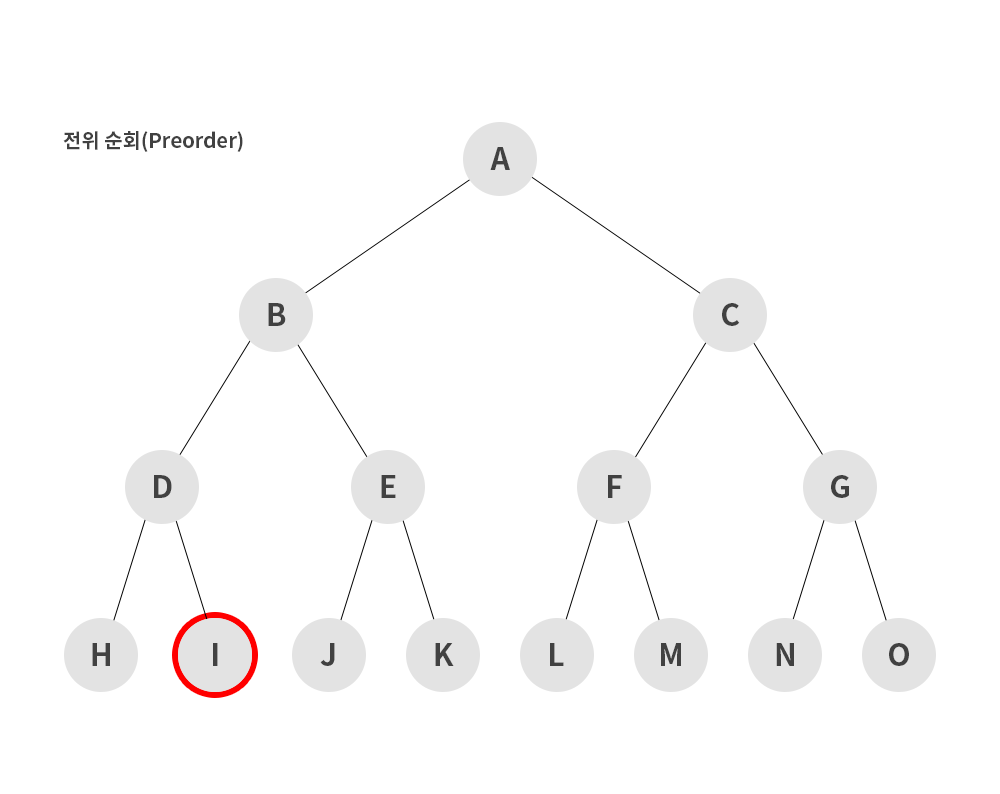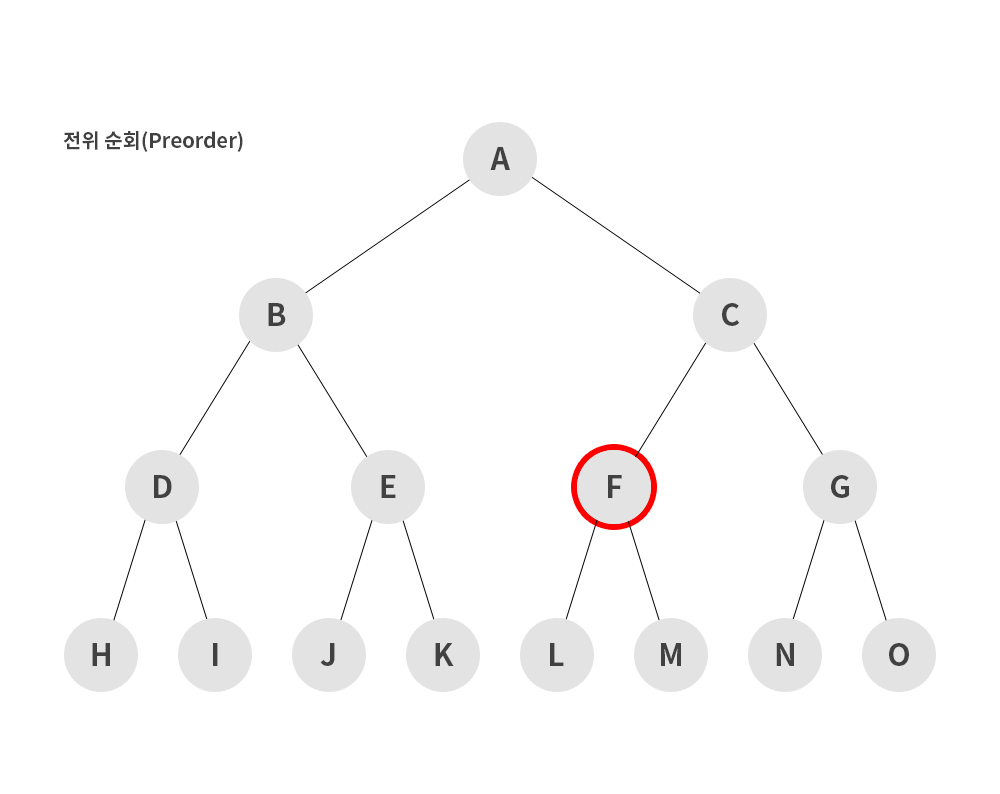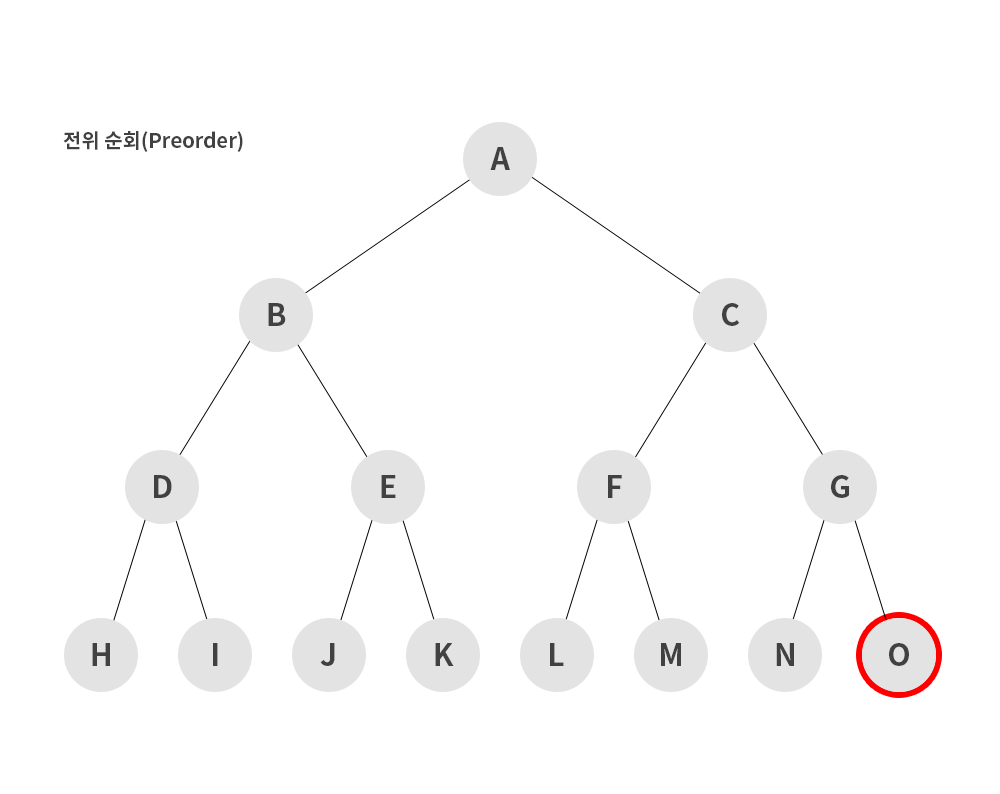
A → B → D → H → I → E → J → K → C → F → L → M → G → N → O
# 백준 1991번 트리 순회 문제 중 일부
def preorder(node):
if node != ".":
print(node, end='')
preorder(tree[node][0])
preorder(tree[node][1])
2) 중위 순회(inorder)
- 왼쪽 서브트리 -> 루트 노드 -> 오른쪽 서브트리 순으로 순회하는 방식
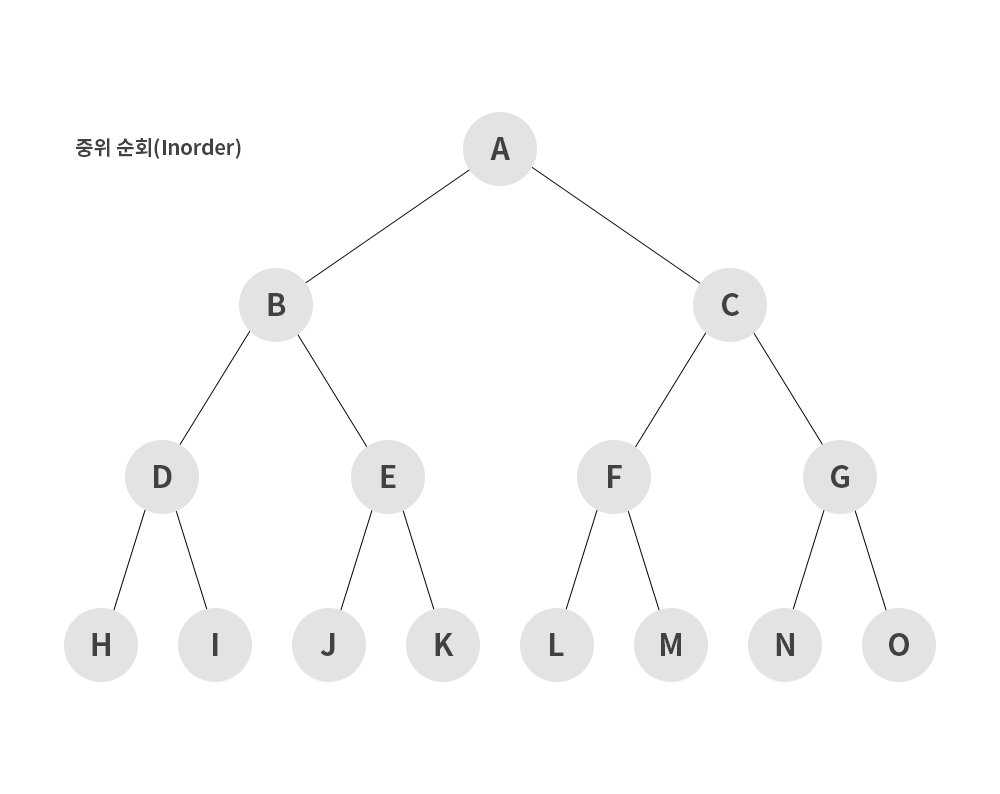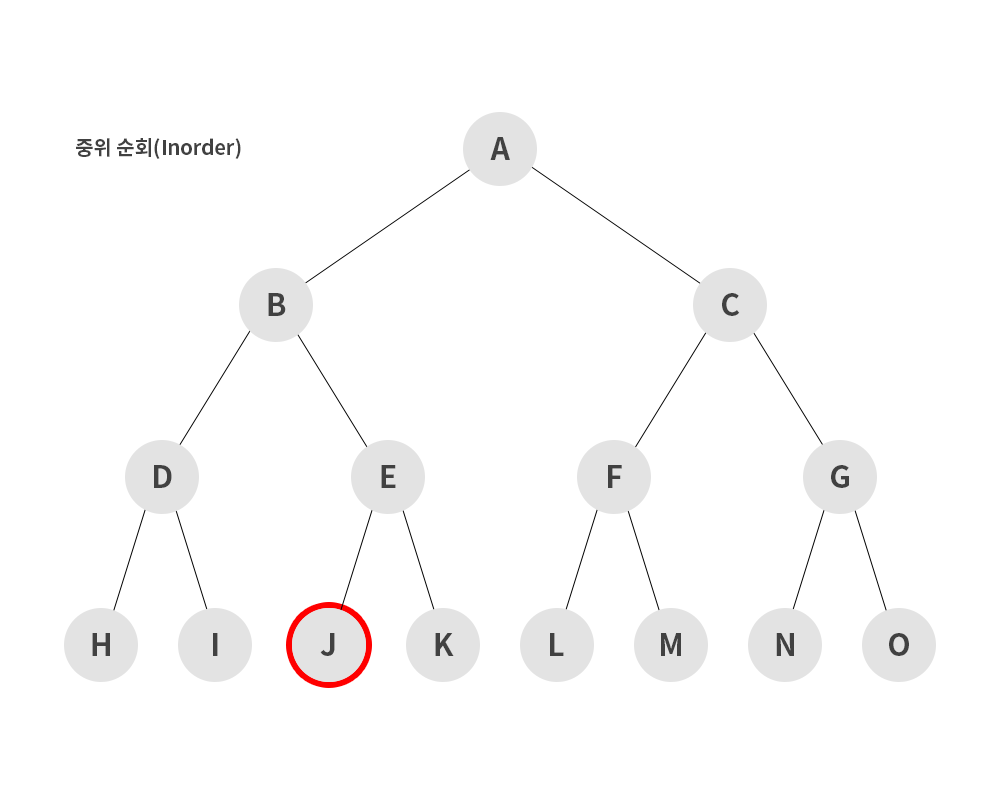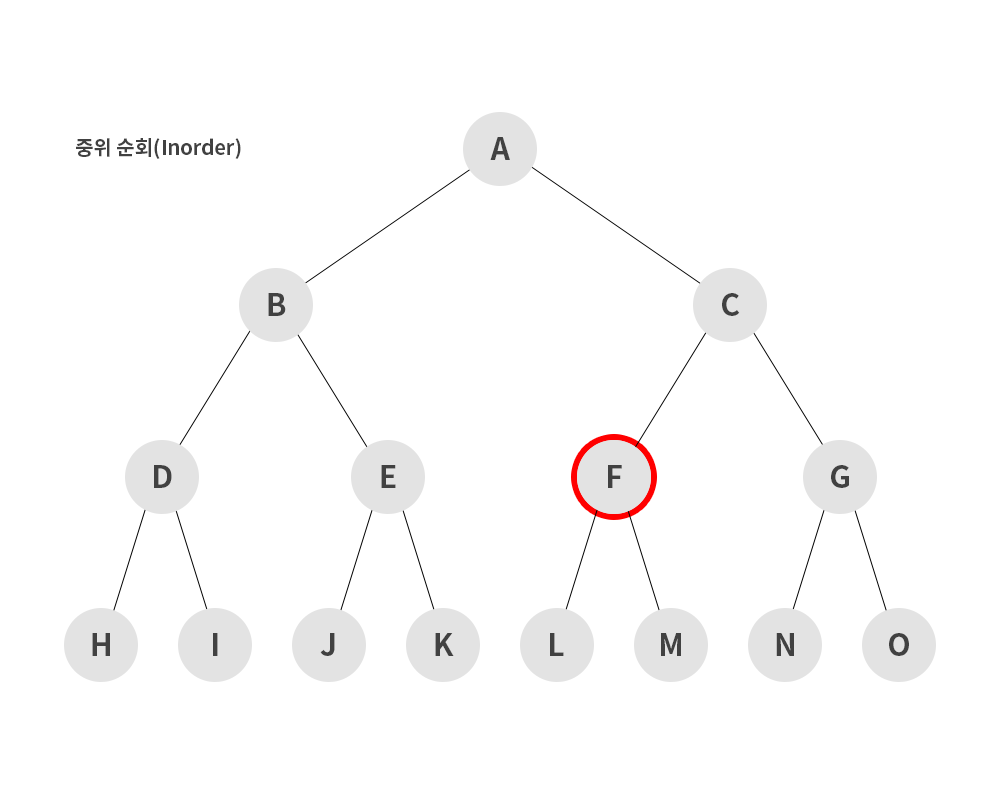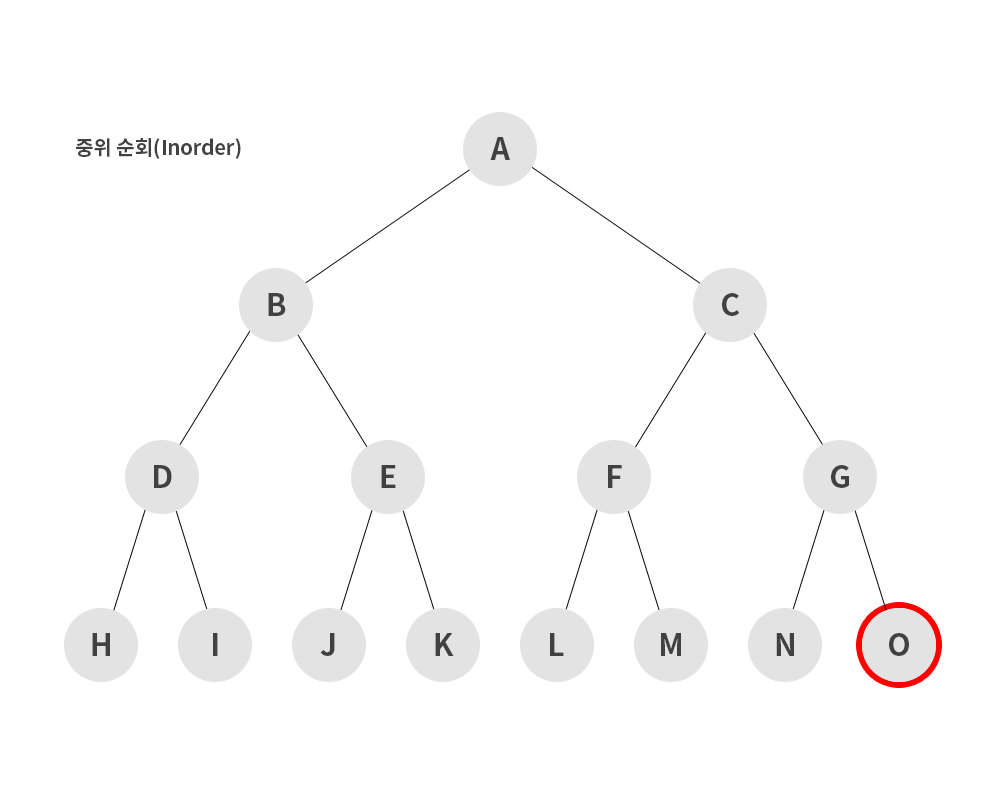
H → D → I → B → J → E → K → A → L → F → M → C → N → G → O
# 백준 1991번 트리 순회 문제 중 일부
def inorder(node):
if node != ".":
inorder(tree[node][0])
print(node, end='')
inorder(tree[node][1])
3) 후위 순회 (postorder)
- 왼쪽 서브트리 -> 오른쪽 서브트리 -> 루트 노드 순으로 순회하는 방식
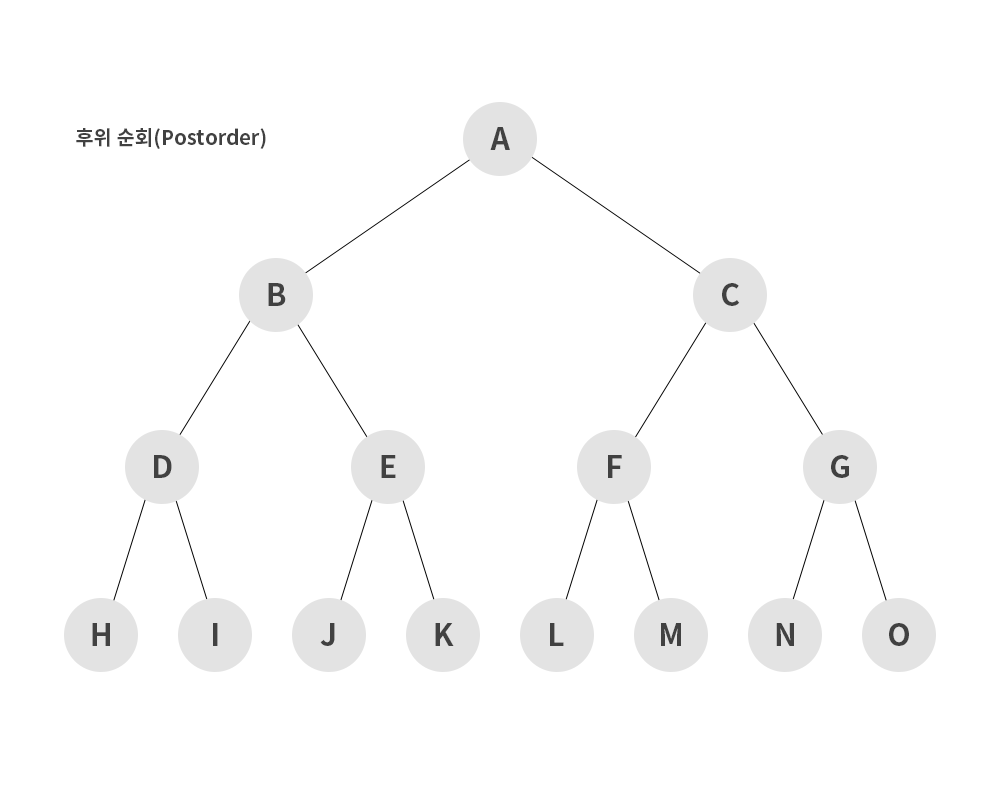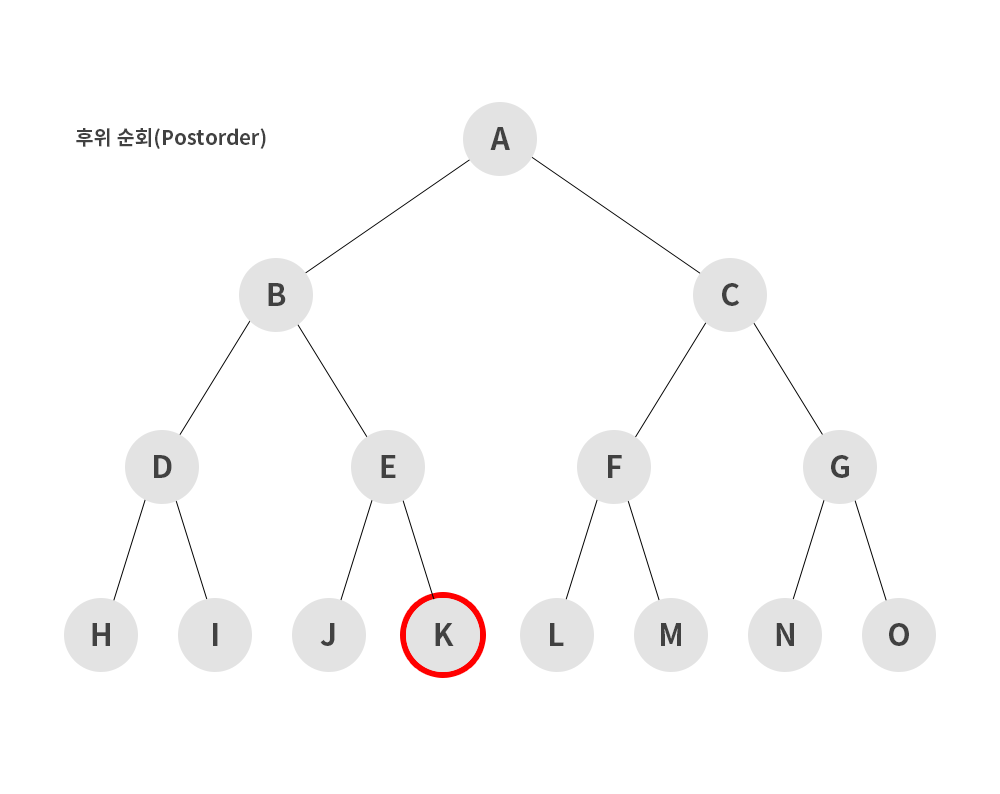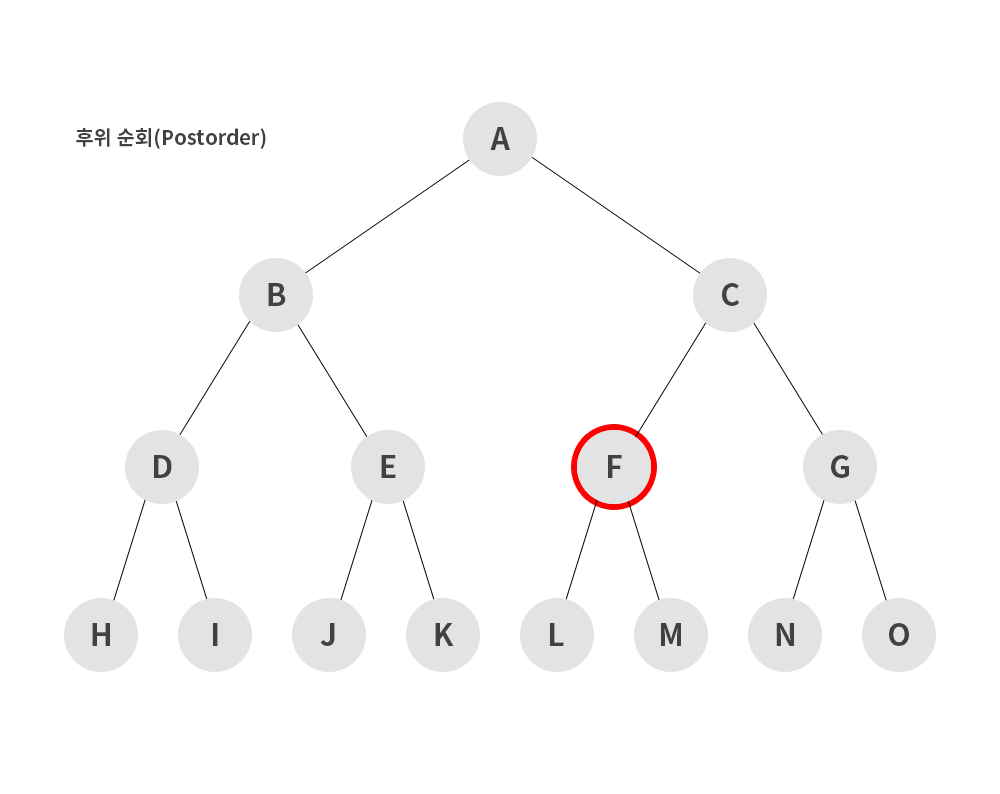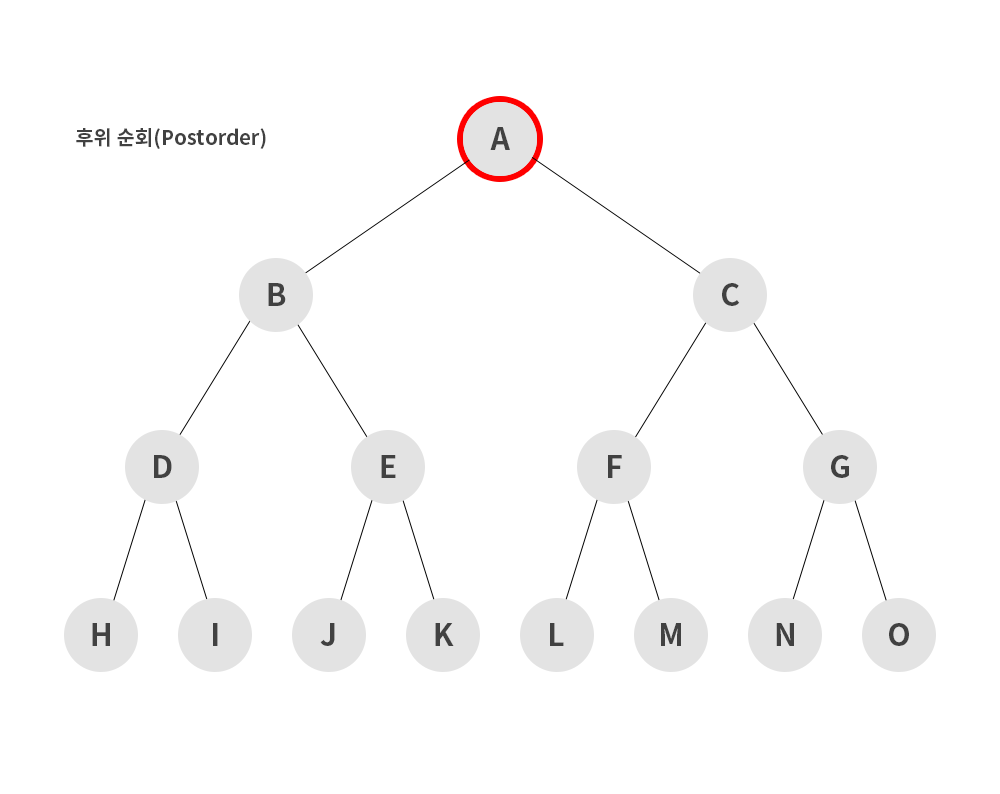
H → I → D → J → K → E → B → L → M → F → N → O → G → C → A
# 백준 1991번 트리 순회 문제 중 일부
def postorder(node):
if node != ".":
postorder(tree[node][0])
postorder(tree[node][1])
print(node, end='')
트리의 종류
이진트리 (Binary Tree)
- 각 노드의 차수가 2 이하인 트리
이진 탐색 트리 (Binary Search Tree)
- 순서화된 이진 트리
- 노드의 왼쪽 자식은 부모의 값보다 작은 값을 가져야 하며 노드의 오른쪽 자식은 부모의 값보다 큰 값을 가져야 한다.
m원 탐색 트리 (m-way search tree)
- 최대 m개의 서브 트리를 갖는 탐색 트리
- 이진 탐색 트리의 확장된 형태로 높이를 줄이기 위해 사용
균형 트리 (balanced Tree, b-tree)
- m원 탐색 트리에서 높이 균형을 유지하는 트리
- height-balanced m-way tree라고도 함
이진 트리 (Binary tree)
트리 자료구조는 여러 유형이 있지만 가장 기본이 되는 트리는 이진 트리 구조라고 한다.
- 이진 트리는 두 개 이하의 자식 노드를 가짐. (하나의 자식 노드만 가지는 것도 가능)
- 두 개의 자식 노드 중에서 왼쪽에 있는 노드는 left node, 오른쪽에 있는 노드는 right node.
이진 트리의 종류
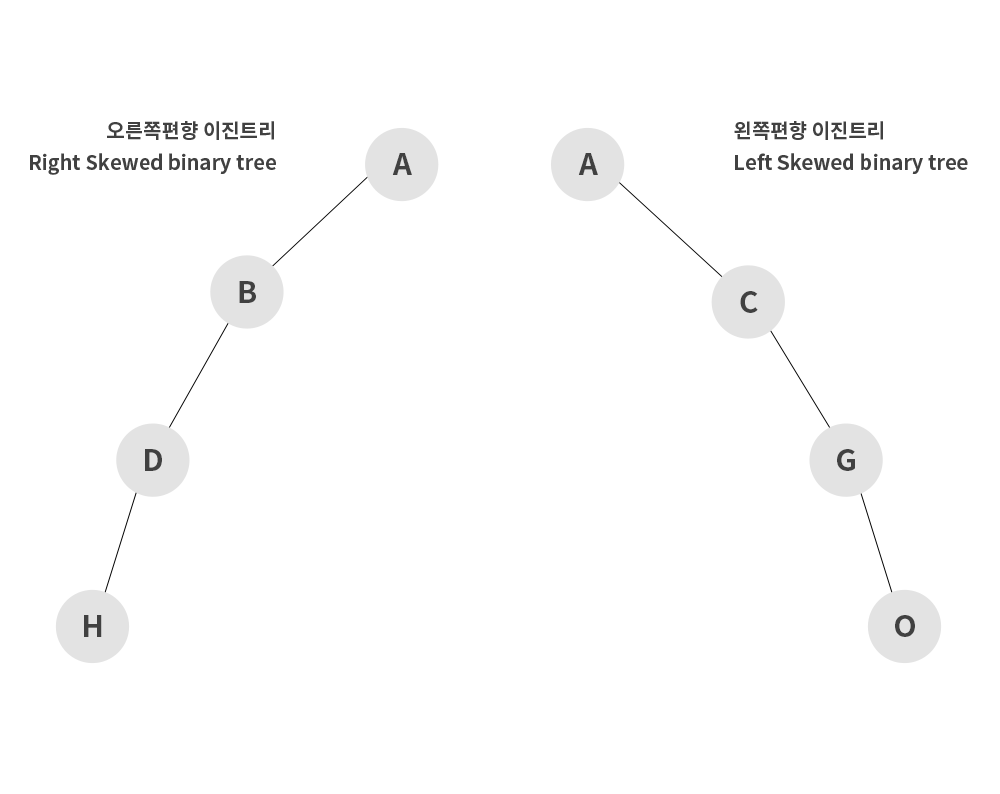
1. 편향 이진 트리 (Skewed binary tree)
편향 이진 트리는 하나의 차수로만 이루어져 있다. 이런 구조는 배열과 같은 선형 구조이기 때문에 leaf node 탐색 시 모두 읽어봐야한다는 단점이 있어서 효율이 떨어진다. 이를 보완하기 위해 높이 균형 트리라는 것이 있다고 한다.
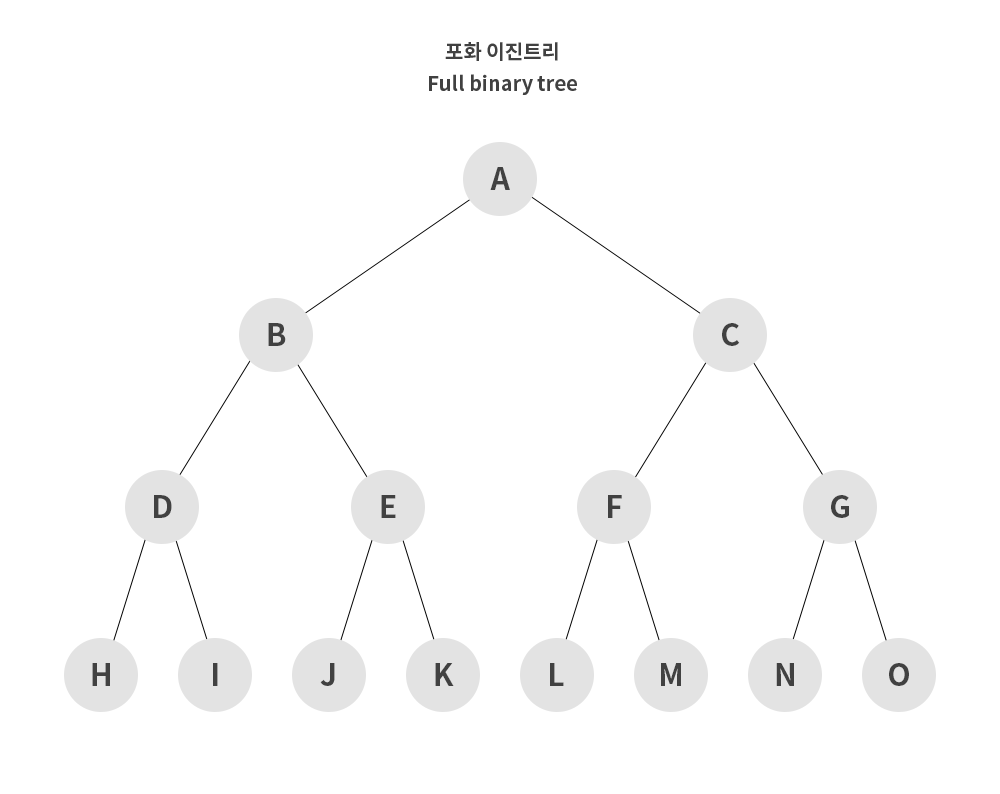
포화 이진 트리 (Full Binary Tree)
포화 이진 트리는 Leaf Node를 제외한 모든 노드의 차수가 두 개로 이루어진 경우를 말한다. 이 경우 해당 차수에 몇 개의 노드가 존재하는지 바로 알 수 있어서 개수 파악이 용이하다는 장점이 있다.
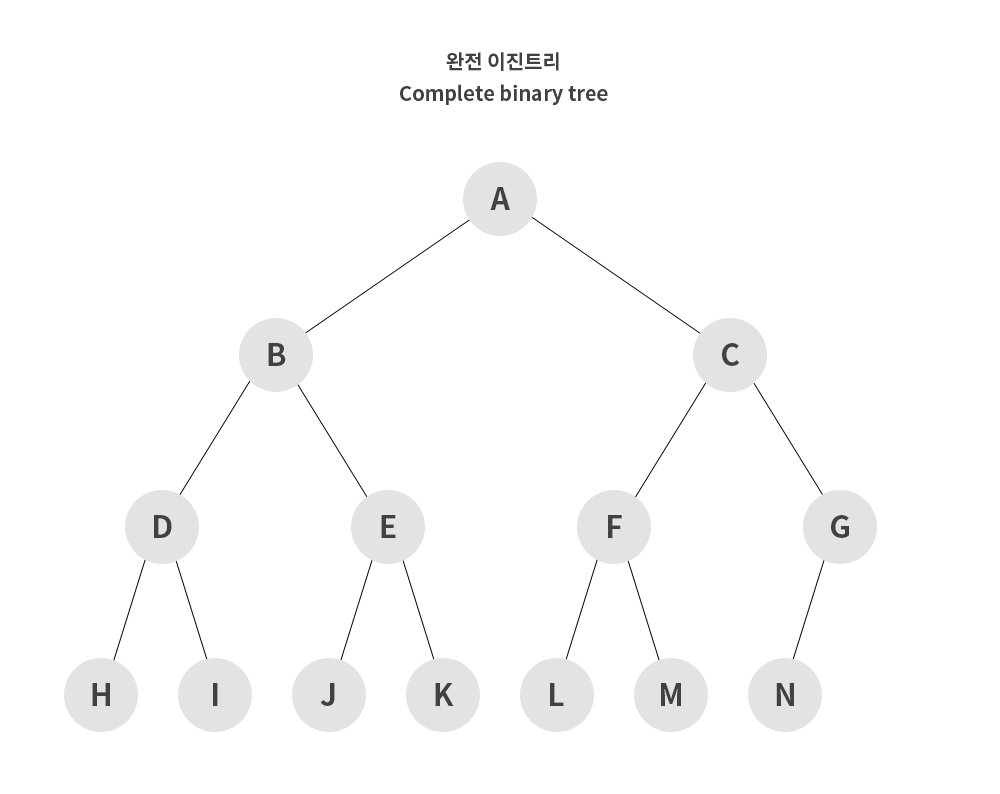
완전 이진 트리 (Complete Binary Tree)
포화 이진 트리와 같은 개념으로 생성하지만 모든 노드가 왼쪽부터 차근차근 생성되는 이진트리를 말한다.
이진 탐색 트리 (Binary Search Tree, BST)
이진 탐색 트리는 탐색을 위한 이진 트리 기반의 자료구조이다. 이진 탐색 트리를 순회할 떄는 중위 순회 방식을 사용한다. (왼쪽 서브트리-루트 노드-오른쪽 서브트리 순으로 순회) 이렇게 하면 이진 탐색 트리 내에 있는 모든 값들을 정렬된 순서로 읽을 수 있다. 다음 예시와 같다.
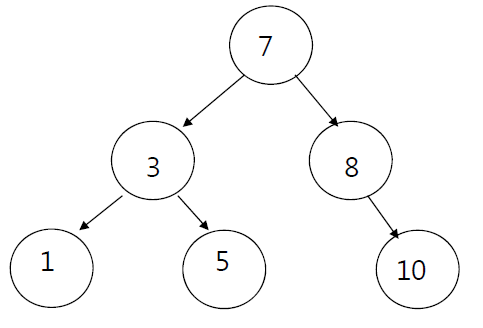
중위순회 : 1, 3, 5, 7, 8, 10
이진 탐색 트리는 다음과 같은 특징이 있다.
- left node에는 parent node보다 작은 값이 저장된다.
- right node에는 parent node보다 크거나 같은 값이 저장된다.
- 모든 노드는 중복된 값을 가지지 않는다.
- 왼쪽 서브트리, 오른쪽 서브트리 또한 이진탐색 트리이다.

이진 탐색 트리를 사용함으로써 데이터를 효율적으로 탐색할 수 있다. 현재의 node 값보다 찾고자 하는 값이 크면 오른쪽으로 움직이고 작으면 왼쪽으로 움직인다.
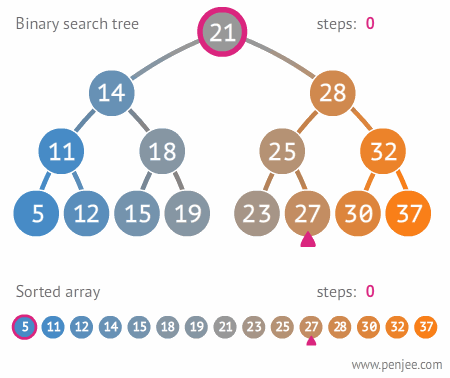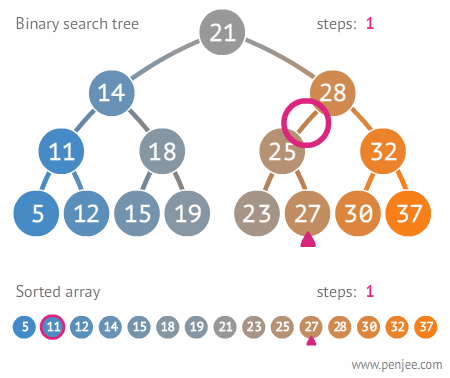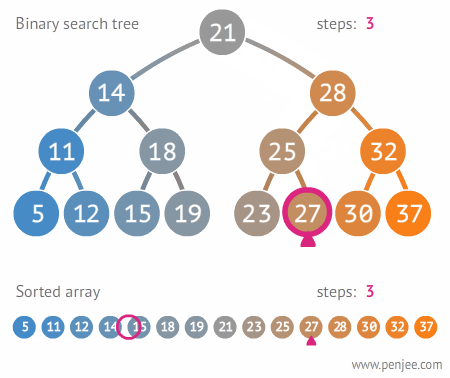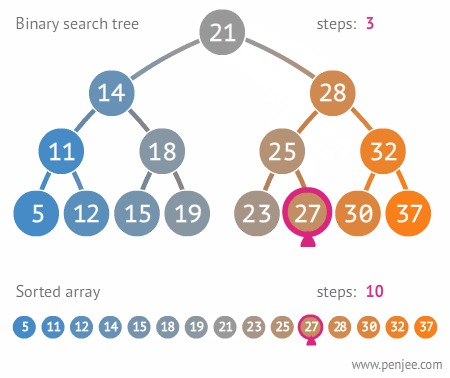
트리가 사용되는 곳
트리는 계층적인 관계 표현에 쓰이기 때문에 윈도우와 리눅스의 파일 시스템 구조나 대용량의 데이터를 계층적으로 저장할 때 많이 사용된다.
계층적 데이터 저장
- 트리는 데이터를 계층 구조로 저장하는 데 사용
- 파일 및 폴더는 계층적 트리 형태로 저장
효율적인 검색 속도
- 효율적인 삽입, 삭제 및 검색을 위해 트리 구조를 사용
힙(Heap)
- 힙은 트리로 구성된 자료 구조
데이터 베이스 인덱싱
- 데이터베이스 인덱싱을 구현하는데 트리를 사용
- ex) B-Tree, B+Tree, AVL-Tree..
Trie
- 사전을 저장하는 데 사용되는 특별한 종류의 트리
참고자료
https://ratsgo.github.io/data%20structure&algorithm/2017/10/22/bst/
이진탐색트리(Binary Search Tree) · ratsgo's blog
이번 글에서는 자료구조의 일종인 이진탐색트리(Binary Search Tree)에 대해 살펴보도록 하겠습니다. 이 글은 고려대 김선욱 교수님, 그리고 역시 같은 대학의 김황남 교수님 강의와 위키피디아를 정
ratsgo.github.io
https://yoongrammer.tistory.com/68
[자료구조] 트리 (Tree)
목차 트리 (Tree) 트리 (Tree)란 노드들이 나무 가지처럼 연결된 비선형 계층적 자료구조입니다. 트리는 다음과 같이 나무를 거꾸로 뒤집어 놓은 모양과 유사합니다. 트리는 또한 트리 내에 다른 하
yoongrammer.tistory.com
https://velog.io/@taeha7b/datastructure-tree
[자료구조] Tree
트리 자료구조는 일반적으로 대상정보의 각 항목들을 계층적으로 구조화 할때 사용하는 비선형 자료구조입니다.
velog.io
'자료구조 및 알고리즘' 카테고리의 다른 글
| [자료구조 및 알고리즘] 배낭 문제와 그 변형 (0) | 2024.08.13 |
|---|---|
| [자료구조 및 알고리즘] 가장 긴 증가하는 부분 수열(Longest Increasing Subsequence, LIS) (0) | 2024.07.15 |
| [자료구조 및 알고리즘] 누적합 (4) | 2024.03.05 |
| [자료구조 및 알고리즘] 서로소 집합 (disjoint set) (0) | 2024.01.22 |
| [자료구조 및 알고리즘] 유클리드 호제법 (0) | 2024.01.19 |
트리
트리는 그래프의 일종으로 노드들이 나무 가지처럼 연결된 비선형 계층적 자료구조이다.

트리 용어

- Node: 트리 구조의 교점으로 node는 데이터를 가지고 있고, 자식 노드를 가질 수 있음.
- Root Node: 트리 구조에서 가장 위에 있는 노드. 즉, 트리의 시작점이 되는 노드.
- Edge: 트리를 구성하기 위해 노드와 노드를 연결하는 선.
- Level: 트리의 특정 깊이를 가지는 노드의 집합.
- Degree: 각 노드가 가진 가지의 수. '차수'라고도 함
- Leaf Node (Terminal Node): 하위에 다른 노드가 연결되어 있지 않은 노드.
- Internal Node: Leaf Node를 제외한, 중간에 위치한 노드들.

트리의 특징
- 트리 자료구조는 일반적으로 대상 정보의 각 항목들을 계층적으로 구조화할 때 사용하는 비선형 자료구조
- Tree 구조는 데이터의 저장의 의미보다는 저장된 데이터를 더 효과적으로 탐색하기 위해 사용
- 리스트와 다르게 데이터가 단순히 나열되는 구조가 아니라, 부모와 자식의 계층적인 관계로 표현
- 트리는 그래프의 한 종류이며 사이클이 없음
- 트리에서 Root Node를 제외한 모든 노드는 단 하나의 부모노드를 가진다.
트리 순회
트리의 순회란 트리의 각 노드를 체계적인 방법으로 탐색하는 과정을 말한다. 노드를 탐색하는 순서에 따라 전위 순회, 중위 순회, 후위 순회 세 가지로 나뉜다.
1) 전위 순회(preorder)
- 루트노드 -> 왼쪽 서브 트리 -> 오른쪽 서브트리 순으로 순회하는 방식

A → B → D → H → I → E → J → K → C → F → L → M → G → N → O
# 백준 1991번 트리 순회 문제 중 일부
def preorder(node):
if node != ".":
print(node, end='')
preorder(tree[node][0])
preorder(tree[node][1])
2) 중위 순회(inorder)
- 왼쪽 서브트리 -> 루트 노드 -> 오른쪽 서브트리 순으로 순회하는 방식

H → D → I → B → J → E → K → A → L → F → M → C → N → G → O
# 백준 1991번 트리 순회 문제 중 일부
def inorder(node):
if node != ".":
inorder(tree[node][0])
print(node, end='')
inorder(tree[node][1])
3) 후위 순회 (postorder)
- 왼쪽 서브트리 -> 오른쪽 서브트리 -> 루트 노드 순으로 순회하는 방식

H → I → D → J → K → E → B → L → M → F → N → O → G → C → A
# 백준 1991번 트리 순회 문제 중 일부
def postorder(node):
if node != ".":
postorder(tree[node][0])
postorder(tree[node][1])
print(node, end='')
트리의 종류
이진트리 (Binary Tree)
- 각 노드의 차수가 2 이하인 트리
이진 탐색 트리 (Binary Search Tree)
- 순서화된 이진 트리
- 노드의 왼쪽 자식은 부모의 값보다 작은 값을 가져야 하며 노드의 오른쪽 자식은 부모의 값보다 큰 값을 가져야 한다.
m원 탐색 트리 (m-way search tree)
- 최대 m개의 서브 트리를 갖는 탐색 트리
- 이진 탐색 트리의 확장된 형태로 높이를 줄이기 위해 사용
균형 트리 (balanced Tree, b-tree)
- m원 탐색 트리에서 높이 균형을 유지하는 트리
- height-balanced m-way tree라고도 함
이진 트리 (Binary tree)
트리 자료구조는 여러 유형이 있지만 가장 기본이 되는 트리는 이진 트리 구조라고 한다.
- 이진 트리는 두 개 이하의 자식 노드를 가짐. (하나의 자식 노드만 가지는 것도 가능)
- 두 개의 자식 노드 중에서 왼쪽에 있는 노드는 left node, 오른쪽에 있는 노드는 right node.
이진 트리의 종류
1. 편향 이진 트리 (Skewed binary tree)
편향 이진 트리는 하나의 차수로만 이루어져 있다. 이런 구조는 배열과 같은 선형 구조이기 때문에 leaf node 탐색 시 모두 읽어봐야한다는 단점이 있어서 효율이 떨어진다. 이를 보완하기 위해 높이 균형 트리라는 것이 있다고 한다.

포화 이진 트리 (Full Binary Tree)
포화 이진 트리는 Leaf Node를 제외한 모든 노드의 차수가 두 개로 이루어진 경우를 말한다. 이 경우 해당 차수에 몇 개의 노드가 존재하는지 바로 알 수 있어서 개수 파악이 용이하다는 장점이 있다.

완전 이진 트리 (Complete Binary Tree)
포화 이진 트리와 같은 개념으로 생성하지만 모든 노드가 왼쪽부터 차근차근 생성되는 이진트리를 말한다.

이진 탐색 트리 (Binary Search Tree, BST)
이진 탐색 트리는 탐색을 위한 이진 트리 기반의 자료구조이다. 이진 탐색 트리를 순회할 떄는 중위 순회 방식을 사용한다. (왼쪽 서브트리-루트 노드-오른쪽 서브트리 순으로 순회) 이렇게 하면 이진 탐색 트리 내에 있는 모든 값들을 정렬된 순서로 읽을 수 있다. 다음 예시와 같다.

중위순회 : 1, 3, 5, 7, 8, 10
이진 탐색 트리는 다음과 같은 특징이 있다.
- left node에는 parent node보다 작은 값이 저장된다.
- right node에는 parent node보다 크거나 같은 값이 저장된다.
- 모든 노드는 중복된 값을 가지지 않는다.
- 왼쪽 서브트리, 오른쪽 서브트리 또한 이진탐색 트리이다.

이진 탐색 트리를 사용함으로써 데이터를 효율적으로 탐색할 수 있다. 현재의 node 값보다 찾고자 하는 값이 크면 오른쪽으로 움직이고 작으면 왼쪽으로 움직인다.

트리가 사용되는 곳
트리는 계층적인 관계 표현에 쓰이기 때문에 윈도우와 리눅스의 파일 시스템 구조나 대용량의 데이터를 계층적으로 저장할 때 많이 사용된다.
계층적 데이터 저장
- 트리는 데이터를 계층 구조로 저장하는 데 사용
- 파일 및 폴더는 계층적 트리 형태로 저장
효율적인 검색 속도
- 효율적인 삽입, 삭제 및 검색을 위해 트리 구조를 사용
힙(Heap)
- 힙은 트리로 구성된 자료 구조
데이터 베이스 인덱싱
- 데이터베이스 인덱싱을 구현하는데 트리를 사용
- ex) B-Tree, B+Tree, AVL-Tree..
Trie
- 사전을 저장하는 데 사용되는 특별한 종류의 트리
참고자료
https://ratsgo.github.io/data%20structure&algorithm/2017/10/22/bst/
이진탐색트리(Binary Search Tree) · ratsgo's blog
이번 글에서는 자료구조의 일종인 이진탐색트리(Binary Search Tree)에 대해 살펴보도록 하겠습니다. 이 글은 고려대 김선욱 교수님, 그리고 역시 같은 대학의 김황남 교수님 강의와 위키피디아를 정
ratsgo.github.io
https://yoongrammer.tistory.com/68
[자료구조] 트리 (Tree)
목차 트리 (Tree) 트리 (Tree)란 노드들이 나무 가지처럼 연결된 비선형 계층적 자료구조입니다. 트리는 다음과 같이 나무를 거꾸로 뒤집어 놓은 모양과 유사합니다. 트리는 또한 트리 내에 다른 하
yoongrammer.tistory.com
https://velog.io/@taeha7b/datastructure-tree
[자료구조] Tree
트리 자료구조는 일반적으로 대상정보의 각 항목들을 계층적으로 구조화 할때 사용하는 비선형 자료구조입니다.
velog.io
'자료구조 및 알고리즘' 카테고리의 다른 글
| [자료구조 및 알고리즘] 배낭 문제와 그 변형 (0) | 2024.08.13 |
|---|---|
| [자료구조 및 알고리즘] 가장 긴 증가하는 부분 수열(Longest Increasing Subsequence, LIS) (0) | 2024.07.15 |
| [자료구조 및 알고리즘] 누적합 (4) | 2024.03.05 |
| [자료구조 및 알고리즘] 서로소 집합 (disjoint set) (0) | 2024.01.22 |
| [자료구조 및 알고리즘] 유클리드 호제법 (0) | 2024.01.19 |
